3cm
4cm
5cm
8cm
15cm
Correct answer is D
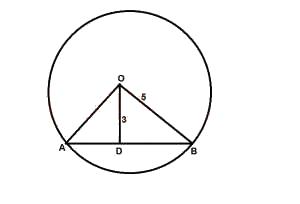
In \(\Delta DOB\), let < DOB = \(\alpha\)
In \(\Delta DOB\), \(5^2 = 3^2 + s^2\)
\(s^2 = 25 - 9 = 16\)
\(s = 4cm\)
\(\sin \alpha = \frac{4}{5}\)
\(\alpha = \frac{< AOB}{2}\)
Length of chord = \(2r \sin (\frac{\theta}{2})\)
|OB| = r = 5cm
L = \(2(5)(\frac{4}{5})\)
= 8 cm
024o
114o
156o
204o
336o
Correct answer is C
tan\(\theta\) = 9/20 = 0.45
\(\theta\) = tan\(^{-1}\) 0.45 = 24.2°
the bearing of y from x = 180 0 - 0 = 180° - 24.2°
the bearing = 155.8°
\(\approxeq\) 156°
If 3\(^y\) = 243, find the value of y.
2
3
4
5
6
Correct answer is D
3\(^y\) = 243;
3\(^y\) = 3\(^5\)
y = 5
21
9
7
4
3
Correct answer is A
Let the integer = y
∴∴ 5y - 2y = 63
3y = 63 ⟹⟹ y = 21
25.7o
44o
51.43o
98o
114.55o
Correct answer is E
L = 14cm, r = 7cm; \(\theta\)= ?
L = \(\frac{\theta}{360}\) x 2πr
14= \(\frac{\theta}{360}\) x 2π(7)
\(\theta = \frac{360 \times 14}{44}\)
=114.55°
WAEC Subjects
Aptitude Tests