In the diagram above, O is the center of the circle. Calc...
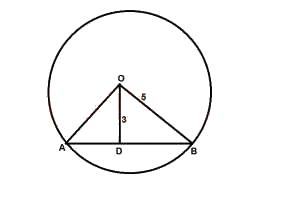
In the diagram above, O is the center of the circle. Calculate the length of the chord AB if |OA| = 5cm, |OD| = 3cm and ∠AOD = ∠BOD
A.
3cm
B.
4cm
C.
5cm
D.
8cm
E.
15cm
Correct answer is D
In ΔDOB, let < DOB = α
In ΔDOB, 52=32+s2
s2=25−9=16
s=4cm
sinα=45
α=<AOB2
Length of chord = 2rsin(θ2)
|OB| = r = 5cm
L = 2(5)(45)
= 8 cm
Similar Questions
In the diagram above, XY = 8cm and OX = 5cm. Find Oz ...
The angles of a polygon are given by 2x, 5x, x and 4x respectively. The value of x is...
Marks 3 4 5 6 7 8 Frequency 5 y - 1 y ...
Simplify 4a2−49b22a2−5ab−7b2...
If the pass mark was 4. What percentage of the pupils failed the test? ...