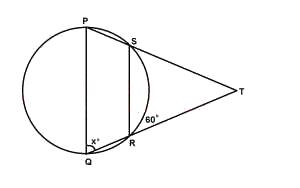
In the diagram above, TR = TS and ∠TRS = 60o. Find the value of x
30
45
60
120
150
Correct answer is C
∠TRS = ∠RST = 60o
∠PSR + ∠PQR = 180o, 120o + xo = 180o
x = 60o
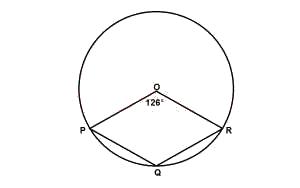
In the diagram above, O is the center of the circle and ∠POR = 126°. Find ∠PQR
234o
117o
72o
63o
54o
Correct answer is B
Reflex < POR = 360° - 126° = 234°
∴ < PQR = \frac{1}{2} \times 234°
= 117°
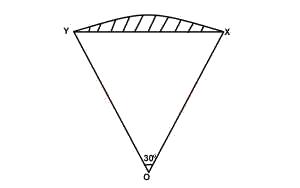
5/12cm2
7/12cm2
11/6cm2
2 1/3cm2
6 1/6cm2
Correct answer is B
Area of \Delta OXY = 12\frac{1}{4} cm^2
Area of sector OXY = \frac{30}{360} \times \frac{22}{7} \times 7 \times 7
= \frac{77}{6} = 12\frac{5}{6} cm^2
Area of the shaded portion = 12\frac{5}{6} - 12\frac{1}{4}
= \frac{7}{12} cm^2
The area of a parallelogram is 513cm^2 and the height is 19cm. Calculate the base.
13.5cm
25cm
27cm
54cm
108cm
Correct answer is C
Area of parallelogram = base \times height.
513 = base \times 19 \implies base = \frac{513}{19}
= 27 cm
WAEC Subjects
Aptitude Tests