In the diagram above PQT is a tangent to the circle QRS a...
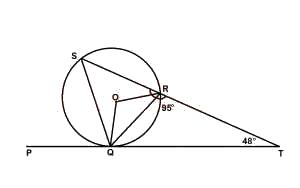
In the diagram above PQT is a tangent to the circle QRS at Q. Angle QTR = 48° and ∠QRT = 95°. Find ∠QRT
A.
48o
B.
45o
C.
37o
D.
32o
E.
30o
Correct answer is C
∠RQT = 180° - (95° + 48°) = 73°
∠OQR = 90° - 37° = 53°
∠QOR = 180° - (53° + 53°) = 74°
QSR = 74°/2 = 37°
Similar Questions
What value of p will make (x2 - 4x + p) a perfect square?...
If (-3, -4) is a point on the line y = mx + 2 find the value of m....
What is the common ratio of the G.P. (√10+√5)+(√10+2√5)+...?...
In the diagram, ZM is a straight line. Calculate the value of x....
If the exterior angles of quadrilateral are yo, (y + 5)o, (y + 10)o and (y + 25)o, find y...