34 sides
30 sides
26 sides
17 sides
15 sides
Correct answer is D
Sum of interior angles in a polygon = \((2n - 4) \times 90°\)
\(\therefore (2n - 4) \times 90° = 30 \times 90°\)
\(\implies 2n - 4 = 30 \)
\(2n = 34 \implies n = 17\)
The polygon has 17 sides.
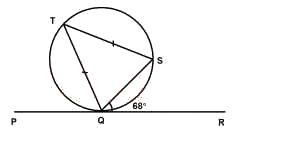
In the diagram, PQR is a tangent to the circle QST at Q. If |QT| = |ST| and ∠SQR = 68°, find ∠PQT.
34o
48o
56o
68o
73o
Correct answer is C
< STQ = < SQR = 68° (alternate segment)
\(\therefore\) < STQ = 68°
< TQS = \(\frac{180° - 68°}{2}\)
= \(\frac{112}{2} = 56°\)
\(\therefore\) < PQT = 180° - (68° + 56°)
= 180° - 124°
= 56°
22cm
33.5cm
43cm
66cm
115.5cm
Correct answer is C
Perimeter of a sector = \(2r + \frac{\theta}{360} \times 2\pi r\)
= \(2(10.5) + \frac{120}{360} \times 2 \times \frac{22}{7} \times 10.5\)
= \(21 + 22\)
= 43 cm
5cm
6cm
10cm
12cm
15cm
Correct answer is C
Area of rhombus = \(\frac{pq}{2}\)
where p and q are the two diagonals of the rhombus.
\(\therefore 60 = \frac{12 \times q}{2}\)
6q = 60 \(\implies\) q = 10 cm
49.5cm3
99cm3
148.5cm3
297cm3
445.5cm3
Correct answer is C
Volume of a cone = \(\frac{1}{3} \pi r^2 h\)
r = 4\(\frac{1}{2}\) cm; h = 14 cm
Volume of cone = \(\frac{1}{3} \times \frac{22}{7} \times \frac{9}{2} \times \frac{9}{2} \times 14\)
= 297 cm\(^3\)
When half- filled, the volume of the water = \(\frac{297}{2} = 148.5 cm^3\)
WAEC Subjects
Aptitude Tests