In the diagram, PQR is a tangent to the circle QST at Q. ...
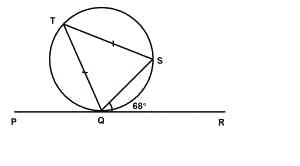
In the diagram, PQR is a tangent to the circle QST at Q. If |QT| = |ST| and ∠SQR = 68°, find ∠PQT.
34o
48o
56o
68o
73o
Correct answer is C
< STQ = < SQR = 68° (alternate segment)
∴ < STQ = 68°
< TQS = \frac{180° - 68°}{2}
= \frac{112}{2} = 56°
\therefore < PQT = 180° - (68° + 56°)
= 180° - 124°
= 56°
Similar Questions
Solve for x and y respectively in the simultaneous equations -2x - 5y = 3. x + 3y = 0...
Solve the simultaneous equation: x+y=2 and 3x-2y=1 ...
Express \frac{2}{x + 3} - \frac{1}{x - 2} as a simple fraction...
Which inequality describes the graph above? ...
Simplify \frac{5^x \times 25^{x - 1}}{125^{x + 1}}...
Calculate the mean deviation of the set of numbers 7, 3, 14, 9, 7, and 8. ...
Tickets for the school play were priced at ₦520.00 each for adults and ₦250.00 each for kids. Ho...