0
1
2
3
4
Correct answer is B
213÷223×117
= 73÷83×87
= 73×38×87
= 1
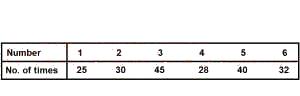
| Number | 1 | 2 | 3 | 4 | 5 | 6 |
| No of times | 25 | 30 | 45 | 28 | 40 | 32 |
A die rolled 200 times. The outcome obtained are shown in the table above.
What is the probability of obtaining a number less than 3 ?
0.125
0.150
0.275
0.500
0.725
Correct answer is C
Prob(less than 3) = 25+30200
= 1140
= 0.275
0.002
0.015
0.15
16
0.2
Correct answer is C
Prob(obtaining a 2) = 30200
= 0.15
What is the probability that the total sum of seven would appear in toss of a fair die?
5/36
1/6
7/36
5/6
1
Correct answer is B
No of possible outcome = 36
Required outcome (R) = {(1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3)}
n(R) = 636
= 16
What is the probability of having an even number in a single toss of a fair die?
1/6
1/3
1/2
2/3
5/6
Correct answer is C
Prob(even number in single toss) = 36
= 12
WAEC Subjects
Aptitude Tests