If \(\frac{2}{x-3}\) - \(\frac{3}{x-2}\) = \(\frac{p}{(x-3)(x -2)}\), find p.
5 - x
- (x + 5)
13 - x
- (5x - 13)
Correct answer is A
\(\frac{2}{x-3}\) - \(\frac{3}{x-2}\)
= \(\frac{2(x -2) -3(x - 3)}{(x-3)(x -2)}\)
= \(\frac{2x -4 -3x + 9}{(x-3)(x -2)}\)
= \(\frac{5 - x}{(x-3)(x -2)}\)
if tanθ = \(frac{3}{4}\), 180° < θ < 270°, find the value of cosθ.
\(\frac{4}{5}\)
\(\frac{3}{5}\)
-\(\frac{4}{5}\)
-\(\frac{3}{5}\)
Correct answer is C
tanθ = \(frac{3}{4}\) → tanθ = 0.75
θ = tan\(^{-1}\)[0.75] → 36.8698°
cosθ = cos[36.8698°]
→ 0.800 or \(frac{4}{5}\)
However; in the third quadrant Cosine is negative
i.e -\(frac{4}{5}\)
Find The quadratic Equation Whose Roots Are -2q And 5q.
3x\(^2\) + 3qx - 10q\(^2\)
x\(^2\) + 3qx + 10q\(^2\)
x\(^2\) - 3qx + 10q\(^2\)
x\(^2\) - 3qx - 10q\(^2\)
Correct answer is D
x\(^2\) - (sum of roots)x + (products of roots) = 0
x\(^2\) - (-2q + 5q) + (-2q * 5q) = 0
x\(^2\) -(3q) + (-10q\(^2\)) = 0
x\(^2\) -3q - 10q\(^2\) = 0
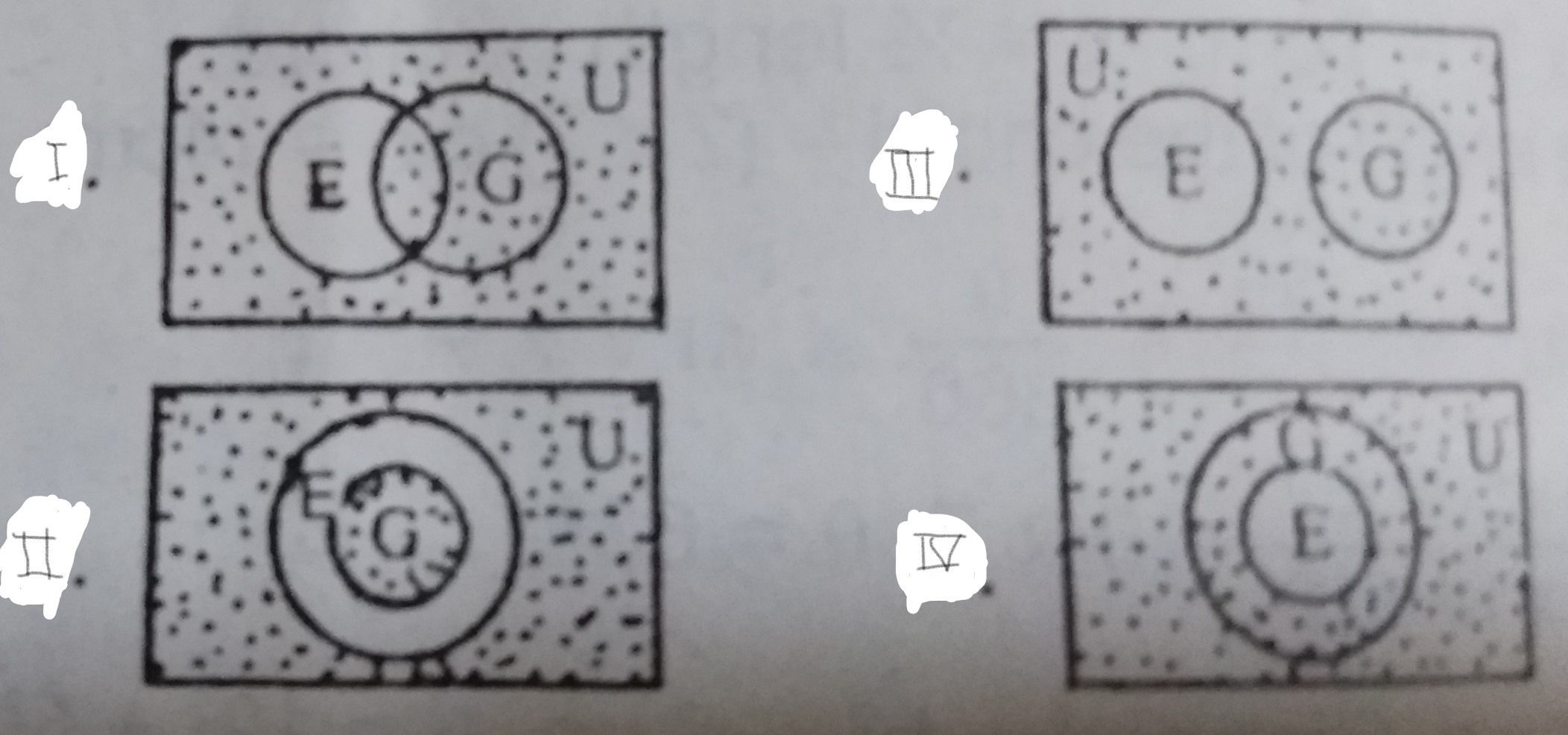
A
B
C
D
Correct answer is C
No explanation has been provided for this answer.
In △LMN, |LM| = 6cm, ∠LNM = x and sin x = sin x = \(\frac{3}{5}\). Find the area of △LMN
60cm\(^2\)
48cm\(^2\)
24cm\(^2\)
30cm\(^2\)
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests