WAEC Mathematics Past Questions & Answers

1,176.

A group of 11 people can speak either English or French or Both. Seven can speak English and six can speak French. What is the probability that a person chosen at random can speak both English and French?

$\frac{2}{11}$

$\frac{4}{11}$

$\frac{5}{11}$

$\frac{11}{13}$

View answer & explanation

Correct answer is A

Let the number of people that speak both English and French = x

Then (7 - x) + x + (6 - x) = 11

13 - x = 11 $\implies$ x = 2.

$\therefore$ P(picking a person that speaks both languages) = 2/11

1,177.

The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below

If he sends $2\frac{1}{2}$ hours week on science, find the total number of hours he studies in a week

$3\frac{1}{3}$ hours

5 hours

8 hours

12 hours

View answer & explanation

Correct answer is D

Let x represent the total number of hours spent per week

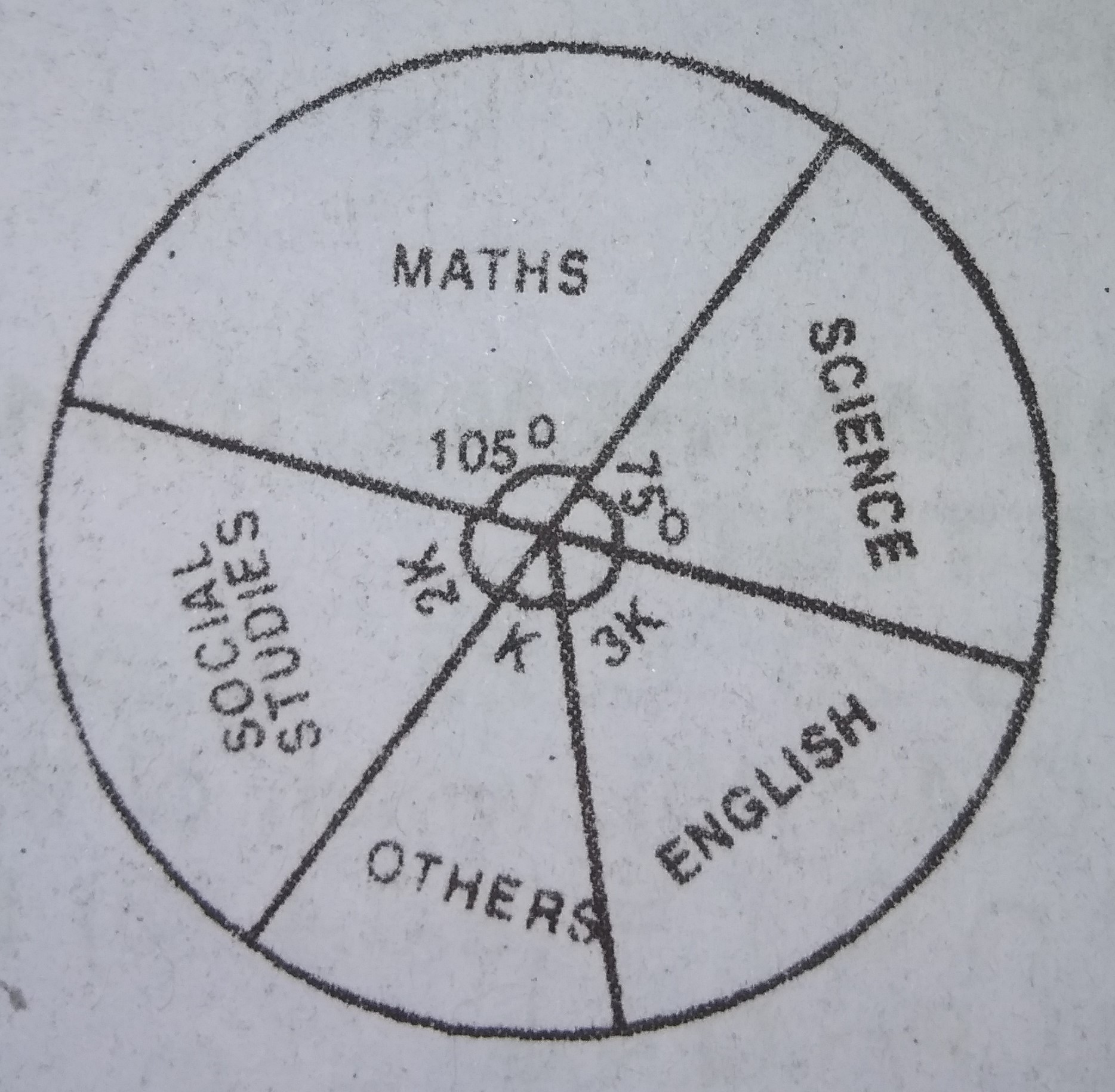
$∴ \frac{75}{360} \times x = \frac{5}{2}$

$∴ x = \frac{360 \times 5}{725 \times 2}=12 hours$

1,178.

The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below Find the value of K

15^o

30^o

60^o

90^o

View answer & explanation

Correct answer is B

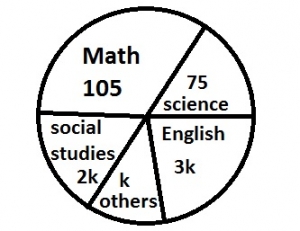
Total angle in a circle = 360°

$\therefore$ 105 + 75 + 2k + k + 3k = 360°

6k = 360 - 180 = 180

k = 180/6 = 30°

1,179.

From a set $A = [3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}]$ , a number is selected at random. Find the probability that is a rational number

$\frac{1}{5}$

$\frac{2}{5}$

$\frac{3}{5}$

$\frac{4}{5}$

View answer & explanation

Correct answer is B

$A = {3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}}$

n(A) = 5

Let the rational nos = R

n(R) = 2 (3, $\sqrt{9}$ )

P(R) = 2/5

1,180.

If $K\sqrt{28}+\sqrt{63}-\sqrt{7}=0$ , find K.

-2

-1

View answer & explanation

Correct answer is B

$K\sqrt{28}+\sqrt{63}-\sqrt{7}=0$

$2K\sqrt{7}+3\sqrt{7}-\sqrt{7}=0$

$2K\sqrt{7}=-2\sqrt{7}$

$K=\frac{-2\sqrt{7}}{2\sqrt{7}}$

$K=-1$

WAEC Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Abstract Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

Verbal Reasoning Questions and Answers

Nigeria General Knowledge Questions and Answers

Spatial Reasoning Questions and Answers

Microsoft Office Questions and Answers

Situational Judgement Questions and Answers

Typing Speed and Accuracy Test

Logical Reasoning Questions and Answers

Quantitative Reasoning Questions and Answers

Puzzles Questions and Answers

Data Interpretation Questions and Answers

Personality Test

See all →

View latest jobs in Nigeria today

WAEC Mathematics Past Questions & Answers - Page 236

WAEC Subjects

Aptitude Tests