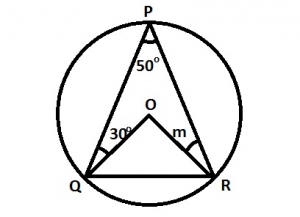
In the diagram, POR is a circle with center O. ∠QPR = 50°, ∠PQO = 30° and ∠ORP = m. Find m.
20o
25o
30o
50o
Correct answer is A
< QOR = 50° x 2 = 100°
Reflex < QOR = 360° - 100° = 260°
∴ 30° + 50° + 260° + m = (4 - 2) x 180°
340° + m = 360°
m = 360° - 340° = 20°
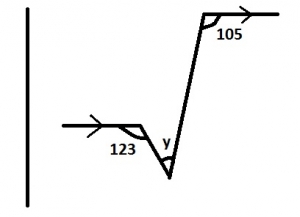
Calculate the value of Y in the diagram
18o
42o
48o
132o
Correct answer is C
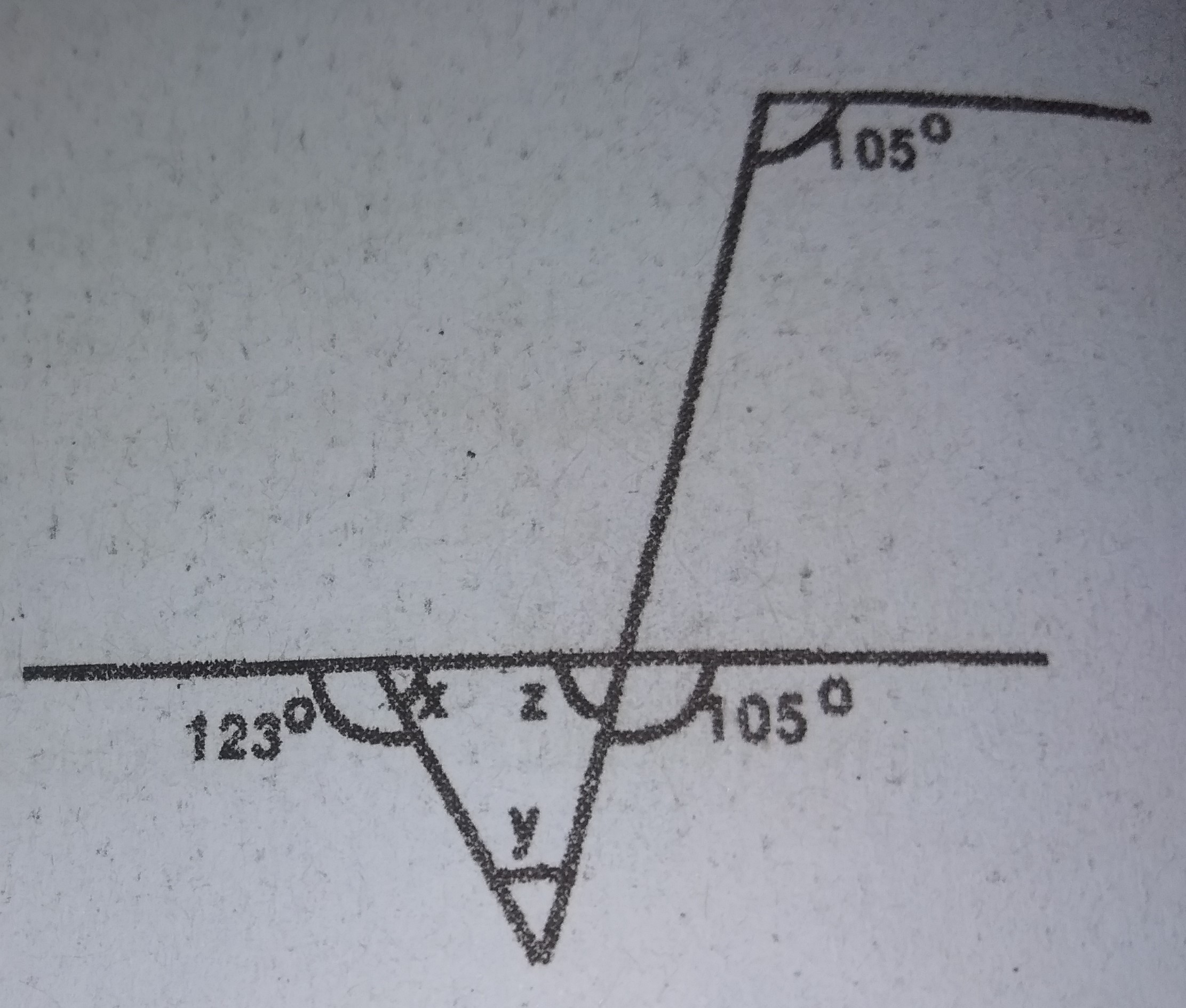
x = 180° - 123° = 57°
z = 180° - 105° = 75°
y = 180° - 57° - 75° = 48°
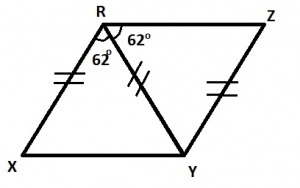
In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = ∠YRZ = 62o, Calculate ∠XYZ
50o
62o
112o
115o
Correct answer is D
In triangle RXY, < RXY = < RYX (base angles of an isosceles triangle)
\implies 180° - 62° = 2 < RYX
118° = 2 < RYX \implies < RYX = 59°
In triangle RYZ, < RZY = 62° (base angles of an isosceles triangle)
\therefore < RYZ = 180° - (62° + 62°)
= 180° - 124° = 56°
\therefore < XYZ = 56° + 59°
= 115°
Which of the following figures have one line of symmetry only?
I. Isosceles triangle
II. Rhombus
III. Kite
I and II only
II and III only
I and III only
I, II, and III
Correct answer is C
Isosceles triangle and Kite shapes have 1 line of symmetry each while the rhombus has 2 lines of symmetry.
The interior angle of a regular polygon is twice the exterior angle. How many sides has the polygon?
5
6
8
9
Correct answer is B
Let the exterior angle = d
Note: Exterior angle + Interior angle = 180°
\implies d + 2d = 180°
3d = 180° \implies d = 60°
Recall, exterior angle = \frac{360}{\text{no of sides}}
\therefore \text{No of sides} = \frac{360}{60}
= 6 sides
WAEC Subjects
Aptitude Tests