In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = &...
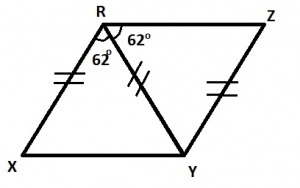
In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = ∠YRZ = 62o, Calculate ∠XYZ
50o
62o
112o
115o
Correct answer is D
In triangle RXY, < RXY = < RYX (base angles of an isosceles triangle)
⟹ 180° - 62° = 2 < RYX
118° = 2 < RYX ⟹ < RYX = 59°
In triangle RYZ, < RZY = 62° (base angles of an isosceles triangle)
∴ < RYZ = 180° - (62° + 62°)
= 180° - 124° = 56°
\therefore < XYZ = 56° + 59°
= 115°
Similar Questions
A student sitting on a tower 68 metres high observes his principal's car at the angle of depress...
\(\begin{array}{c|c} Scores & 3 & 6 & 5 & 2 \\ \hline Frequency & 2 & 3 &...
\(\begin{array}{c|c} \text{Age in years} & 13 & 14 & 15 & 16 & 17 \\ \hline \tex...
Find the area of the sector of a circle with radius 3m, if the angle of the sector is 60o...
If (159.75)10 = (x)6. Find x ...