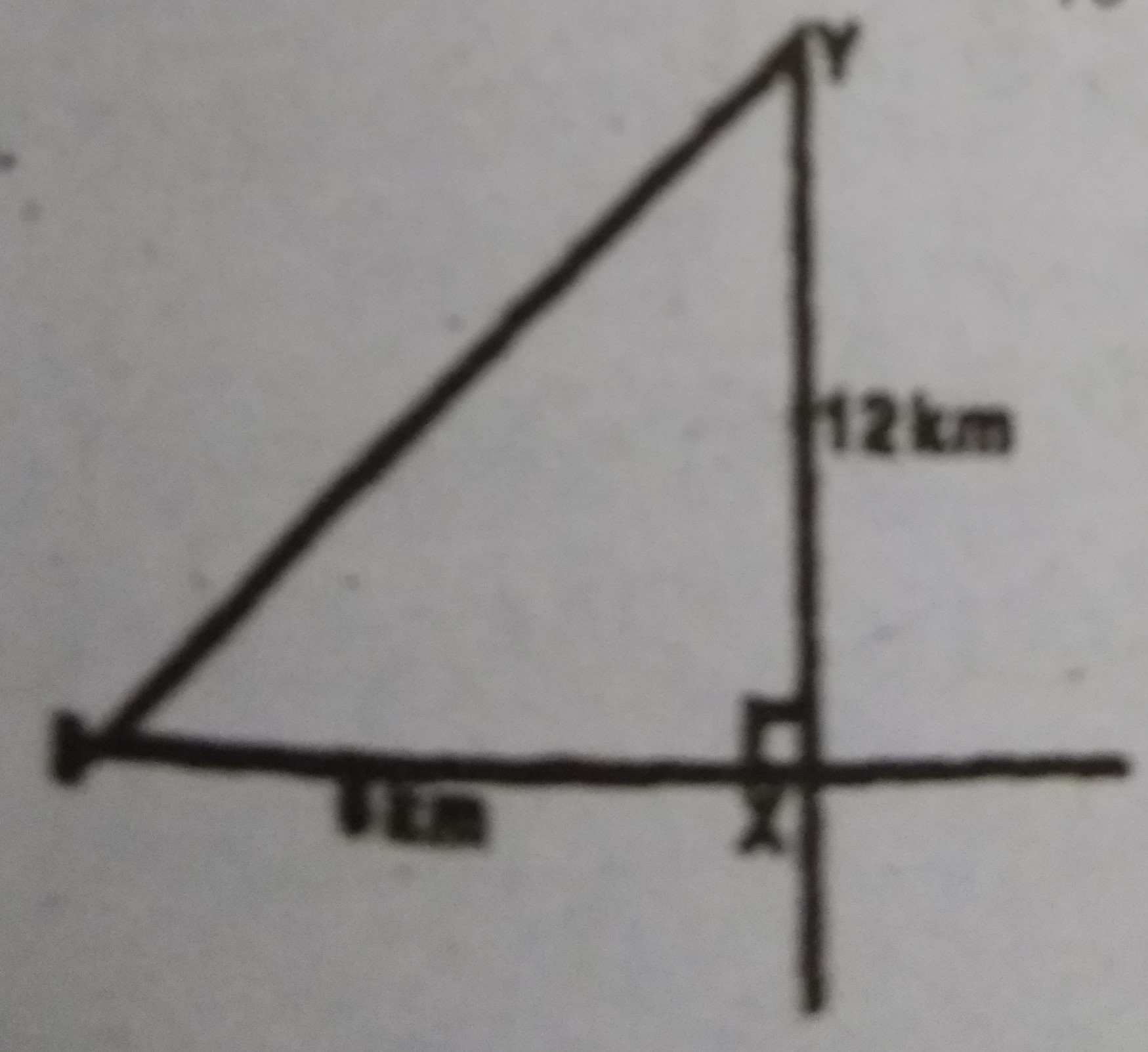
If (x + 3) varies directly as y and x = 3 when y = 12, what is the value of x when y = 8?
1
12
−
-1
Correct answer is A
(x+3) \propto y\\
∴x + 3 = ky\hspace{1mm}when\hspace{1mm}x = 3, y = 12\\
3+3 = 12k\\
∴ k = \frac{1}{2}\\
\Longrightarrow x + 3 = \frac{1}{2}y to find x when y = 8
x + 3 = \frac{1}{2}\times 8\\
x=4-3\\
x = 1
2
3
7
9
Correct answer is B
20 members in the ratio 3:1
Number of women = \frac{1}{4} \times 20
= 5
Let the number of women to be added = x
Total number of members in the committee = 20 + x
\frac{5 + x}{20 + x} = \frac{2}{5}
5(5 + x) = 2(20 + x)
25 + 5x = 40 + 2x \implies 5x - 2x = 40 - 25
3x = 15 \implies x = 5
If log 2 = 0.3010 and log 2^y = 1.8062, find; correct to the nearest whole number, the value of y.
6
5
4
-5
Correct answer is A
log2 = 0.3010\hspace{1mm}given\\ log2^y = 1.8062\\ ∴ ylog2 = 1.8062\\ y=\frac{1.8062}{logy}=\frac{1.8062}{0.3010}=6
4
5
13
17
Correct answer is B
(x + 2)^{2} = x^{2} + (x + 1)^{2}
x^2 + 4x + 4 = x^2 + x^2 + 2x + 1
2x^{2} - x^{2} + 2x - 4x + 1 - 4 = 0
x^{2} - 2x - 3 = 0
x^{2} - 3x + x - 3 = 0 \implies x(x - 3) + 1(x - 3) = 0
(x - 3)(x + 1) = 0 \implies \text{x = 3 or -1}
x > 0 \implies x = 3
The longest side = 3 + 2 = 5.
WAEC Subjects
Aptitude Tests