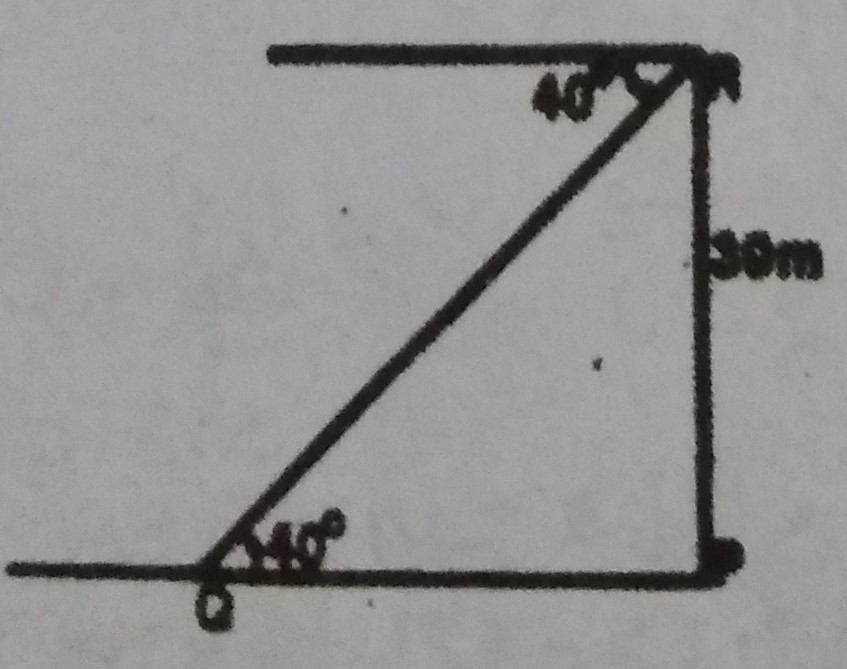
1,012.
A.
7√3
B.
10√3
C.
14√3
D.
18√3
Correct answer is C
3√12+10√3−6√3
= 3(√4×3)+10√3−(6√3)(√3√3)
= 6√3+10√3−2√3
= 14√3
1,013.
The volume of a cylinder of radius 14cm is 210cm3. What is the curved surface area of the cylinder?
A.
15cm2
B.
30cm2
C.
616cm2
D.
1262cm2
Correct answer is B
V=πr2h210=227×142×hh=21022×28
Curved surface area =2rπh=2×227×14×21022×26=30cm2
1,015.
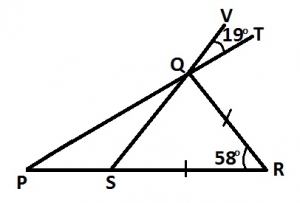

A.
42o
B.
39o
C.
38o
D.
30o
Correct answer is A
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests