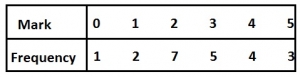
1
2
3
4
Correct answer is C
Median = 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5
Median mark = \(\frac{3+3}{2} = \frac{6}{2} = 3\)
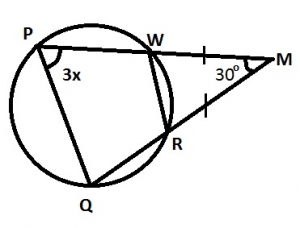
10o
25o
35o
60o
Correct answer is B
MPQ = PQM = 3x; ∆MPQ
MPQ + PQM + PMQ = 180° 3x + 3x + 30° = 180°
\(6x \times 30° = 180° 6x + 180° - 30°; 6x + 150°\)
\(x = \frac{150}{6} = 25^{\circ}\)
Given that \(\sqrt{128}+\sqrt{18}-\sqrt{K} = 7\sqrt{2}\), find K,
8
16
32
48
Correct answer is C
\(\sqrt{128} +\sqrt{18}-\sqrt{k}=7\sqrt{2}\\
\sqrt{2\times 64}+\sqrt{9\times 2} - \sqrt{k} = 7\sqrt{2}\\
8\sqrt{2} + 3\sqrt{2} - \sqrt{k} = 7\sqrt{2}; 11\sqrt{2} - \sqrt{k} = 7\sqrt{2}\\
-\sqrt{k}=7\sqrt{2}-11\sqrt{2}; -\sqrt{k} = -4\sqrt{2}; \sqrt{k}=4\sqrt{2}\\
=\sqrt{4^2\times 2} = \sqrt{16\times 2}; \sqrt{k}=\sqrt{32}; k = 32\)
Find the average of the first four prime numbers greater than10
20
19
17
15
Correct answer is D
First four prime numbers greater than 10 are 11, 13, 17, 19
The average \(= \frac{11+13+17+19}{4}=15\)
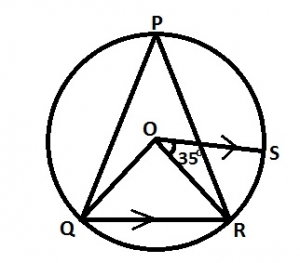
In the diagram, O is the centre of the circle where OS//QR and ∠SOR = 35o
35o
45o
55o
70o
Correct answer is C
∠SOR = ∠ORQ alternate angle.
Also ∠OQR = ∠OQR (Base angle of isosceles)
∠QOR = 108 – 2(35o) = 180 - 70o - 110o ∠QPR = 1/2QOR = 1/2(110o) ∠QPR + 55o (theorem angle at center is twice angle at circumference)
WAEC Subjects
Aptitude Tests