Processing math: 4%

WAEC Mathematics Past Questions & Answers - Page 184

916.

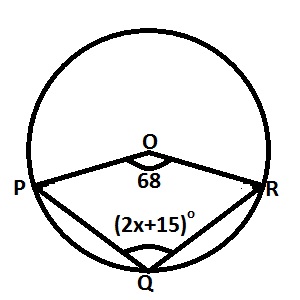
The diagram is a circle centre O. Find the value of x

30^o

50^o

61^o

78^o

65.5 $^{\circ}$

View answer & explanation

Correct answer is E

∠PQR (Reflex) = 360° – 68° = 292°
∠PQR = 2∠PQR
292° = 4x + 30°
4x = 292 – 30 = 262
$x = \frac{262}{4}=65.5°$

917.

Simplify $\frac{2}{a+b}-\frac{1}{a-b}$

$\frac{3}{a+b}$

$\frac{a-3b}{a^2-b^2}$

$\frac{3a-b}{a^2 – b^2}$

$\frac{a-3b}{a^2+b^2}$

View answer & explanation

Correct answer is B

Simplify $\frac{2}{a+b}-\frac{1}{a-b}; \frac{2(a-b)-1(a+b)}{(a+b)(a-b)}$

= $\frac{2a-2b-a-b}{(a+b)(a-b)}$

= $\frac{a-3b}{a^2 - ab + ab - b^2}$

= $\frac{a-3b}{a^2-b^2}$

918.

A boy walks 800m in 20 minutes. Calculate his average speed in km per hour

2.4

View answer & explanation

Correct answer is A

$Average \hspace{1mm}speed = \frac{Distance}{Time\hspace{1mm} taken}\\ Distance = 800m = \frac{800}{1000}km = 0.8km\\ Time\hspace{1mm}taken = 20\hspace{1mm}minutes = \frac{20}{60}hr=\frac{1}{3}hr\\Average \hspace{1mm} speed = \left(0.8\div \frac{1}{3}\right)km/hr = (0.8\times3)km/hr\\=2.4km/hr$

919.

Find the range of values of x for which $\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}$

x > 4

x > -4

x < 4

x < -4

View answer & explanation

Correct answer is D

$\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\\ \frac{3(x+2)-4(x+1)>6}{12}; 3x + 6 – 4x – 4 > 6\ -x +2>6; -x > 4; x < -4$

920.

The table above gives the marks scored by a group of students in a test Use the table to answer the Question below
What is the probability of selecting a student from the group that scored 2 or 3?

$\frac{1}{11}$

$\frac{5}{22}$

$\frac{7}{22}$

$\frac{6}{11}$

View answer & explanation

Correct answer is D

Prob (2 or 3) = prob(2) + prob(3)
Prob (mark 2) $=\frac{7}{22}$ + Prob(mark 3) = $\frac{5}{22}$
Prob(2 or 3) $=\frac{7}{22}+\frac{5}{22}=\frac{12}{22}=\frac{6}{11}$