Make f the subject of the relation \(v = u + ft\)
\(\frac{v-u}{t}\)
\(\frac{u-v}{t}\)
\(t(v+u\)
\(\frac{v}{u}-t\)
Correct answer is A
\(v=u+ft \Rightarrow v-u=ft\Rightarrow f=\frac{v-u}{t}\)
\(2x^2 + 13xy - 15y^2\)
\(2x^2 - 13xy - 15y^2\)
\(2x^2 + 13xy + 15y^2\)
\(2x^2 - 13xy + 15y^2\)
Correct answer is D
\((2x-3y)(x-5y)=2x^2 - 10xy - 3xy + 15y^2\\
=2x^2 - 13xy + 15y^2\)
Solve the equation \(2^7 = 8^{5-x}\)
\(\frac{5}{8}\)
\(\frac{8}{3}\)
\(\frac{3}{2}\)
\(\frac{15}{4}\)
Correct answer is B
\(2^7 = 2^{3(5-x)}\Rightarrow 7 = 3^{5-x} \Rightarrow 7 15 - 3x\\
\Rightarrow -8 = -3x \Rightarrow x = \frac{8}{3}\)
Convert 101101two to a number in base ten
61
46
45
44
Correct answer is C
1011012 = 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 32 + 0 + 8 + 4 + 0 + 1 = 4510
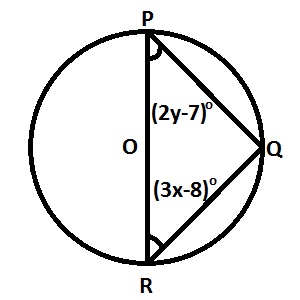
In the diagram, PR is a diameter, ∠PRQ = (3x-8)° and ∠RPQ = (2y-7)°. Find x in terms of y
\(x=\frac{75-2y}{3}\)
\(x=\frac{105-3y}{2}\)
\(x=\frac{105-2y}{3}\)
\(x=\frac{75-3y}{2}\)
Correct answer is C
180 = ∠RPQ + ∠PRQ + ∠PQR Since PQR = 90 (theorem: angle in a semi circle)
180 = ∠RPQ + ∠PRQ + 90 => 180° = (3x-8)°+(2y-7)°+90°; 90+8+7 = 3x+2y =>\(\frac{105-2y}{3}=x\)
WAEC Subjects
Aptitude Tests