In the diagram, PR is a diameter, ∠PRQ = (3x-8)° ...
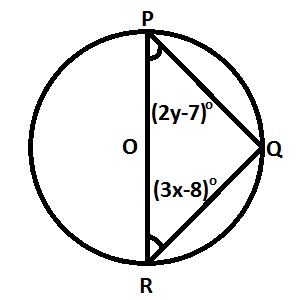
In the diagram, PR is a diameter, ∠PRQ = (3x-8)° and ∠RPQ = (2y-7)°. Find x in terms of y
A.
x=75−2y3
B.
x=105−3y2
C.
x=105−2y3
D.
x=75−3y2
Correct answer is C
180 = ∠RPQ + ∠PRQ + ∠PQR Since PQR = 90 (theorem: angle in a semi circle)
180 = ∠RPQ + ∠PRQ + 90 => 180° = (3x-8)°+(2y-7)°+90°; 90+8+7 = 3x+2y =>105−2y3=x