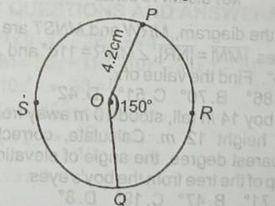
Find the area of the sector OPSQ
15.40cm2
17.64cm2
23.10cm2
32.34cm2
Correct answer is D
\frac{θ}{360} *π * r^2 → \frac{210 * 22 * 4.2 * 4.2}{360 * 7}
\frac{1617}{50} = 32.34cm^2
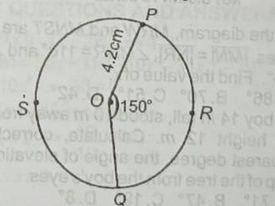
In the diagram, ∠POQ = 150 and the radius of the circle PSQR is 4.2cm. [take π = 22/7]
What is the length of the minor arc?
11cm
15.4cm
17.64cm
23.10cm
Correct answer is A
\frac{θ}{360} * 2 * π * r → \frac{150 * 2 * 22 * 4.2}{360 x 7}
= 11cm
An exterior angle of a regular polygon is 22.5°. Find the number of sides.
13
14
15
16
Correct answer is D
The sum of exterior angles of a polygon is 360°
\frac{360}{22.5} = 16 sides
Make t the subject of k = m \sqrt \frac{t-p}{r}
\frac{k^2r + p}{m^2}
\frac{k^2r + pm^2}{m^2}
\frac{k^2r - p}{m^2}
\frac{k^2r + p^2}{m^2}
Correct answer is B
square both sides to remove the square root
k^2 = m^2 \frac{t-p}{r}
\frac{k^2r}{m^2} = t - p
t = \frac{k^2r}{m^2} + p
t = \frac{k^2r + pm^2}{m^2}
Find the value of x such that \frac{1}{x} +\frac{4}{3x} - \frac{5}{6x} + 1 = 0
\frac{1}{6}
\frac{1}{4}
\frac{-3}{2}
\frac{-7}{6}
Correct answer is C
\frac{1}{x} +\frac{4}{3x} - \frac{5}{6x} + 1 = 0
using 6x as lcm
→ \frac{6+8-5+6x}{6x}
→ \frac{9+6x}{6x} = 0
9+6x = 0
6x = -9
x = \frac{-9}{6} or \frac{-3}{2}
WAEC Subjects
Aptitude Tests