80o
70o
60o
50o
Correct answer is D
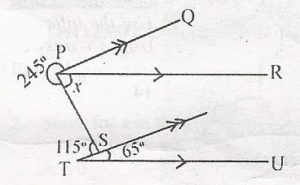
< QPR = < STU = 65o (Corresponding angles)
245 + < QPR = x = 360o (< s at a point)
i.e. 245 + 65 + x = 360
x = 360 - (245 + 65)
x = 360 - 310
x = 50o

7
9
11
13
Correct answer is A
student that like swimming = x + 2
where 2 is the number of students who like reading, dancing and swimming. To find x from the venn diagram of swimming
6 +3 + 2 + x = 16
11 + x = 16
x = 16 - 11 = 5
no. of students that like dancing and swimming
x + 2 = 5 + 2 = 7
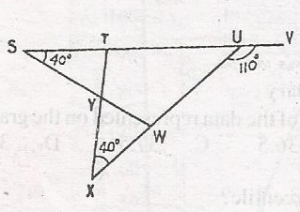
In the diagram, STUV is a straight line. < TSY = < UXY = 40o and < VUW = 110o. Calculate < TYW
150o
140o
130o
120o
Correct answer is A
< TUW = 110o = 180o (< s on a straight line)
< TUW = 180o - 110o = 70o
In \(\bigtriangleup\) XTU, < XUT + < TXU = 180o
i.e. < YTS + 70o = 180
< XTU = 180 - 110o = 70o
Also < YTS + < XTU = 180 (< s on a straight line)
i.e. < YTS + < XTU - 180(< s on straight line)
i.e. < YTS + 70o = 180
< YTS = 180 - 70 = 110o
in \(\bigtriangleup\) SYT + < YST + < YTS = 180o(Sum of interior < s)
SYT + 40 + 110 = 180
< SYT = 180 - 150 = 30
< SYT = < XYW (vertically opposite < s)
Also < SYX = < TYW (vertically opposite < s)
but < SYT + < XYW + < SYX + < TYW = 360
i.e. 30 + 30 + < SYX + TYW = 360
but < SYX = < TYW
60 + 2(< TYW) = 360
2(< TYW) = 360o - 60
2(< TYW) = 300o
TYW = \(\frac{300}{2}\) = 150o
< SYT
i and iii
i and iv
ii and iii
ii and ic
Correct answer is A
No explanation has been provided for this answer.
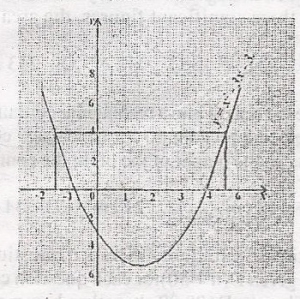
y = 0.5
x = 1.0
x = 1.5
y = 4.6
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests