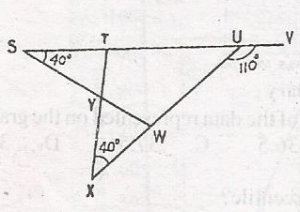
In the diagram, STUV is a straight line. < TSY = < UXY = 40o and < VUW = 110o. Calculate < TYW
150o
140o
130o
120o
Correct answer is A
< TUW = 110o = 180o (< s on a straight line)
< TUW = 180o - 110o = 70o
In △ XTU, < XUT + < TXU = 180o
i.e. < YTS + 70o = 180
< XTU = 180 - 110o = 70o
Also < YTS + < XTU = 180 (< s on a straight line)
i.e. < YTS + < XTU - 180(< s on straight line)
i.e. < YTS + 70o = 180
< YTS = 180 - 70 = 110o
in △ SYT + < YST + < YTS = 180o(Sum of interior < s)
SYT + 40 + 110 = 180
< SYT = 180 - 150 = 30
< SYT = < XYW (vertically opposite < s)
Also < SYX = < TYW (vertically opposite < s)
but < SYT + < XYW + < SYX + < TYW = 360
i.e. 30 + 30 + < SYX + TYW = 360
but < SYX = < TYW
60 + 2(< TYW) = 360
2(< TYW) = 360o - 60
2(< TYW) = 300o
TYW = 3002 = 150o
< SYT
Similar Questions
If m : n = 2 : 1, evaluate 3m2−2n2m2+mn...
In a town of 6250 inhabitants, there were 62 births during 1984. Find the percentage birth rate ...
A ladder leans against a vertical wall at an angle 60° to the wall, if the foot of the ladder is...
Simplify 2.250.015 leaving your answer in standard form...
Simplify 1x−2 + 1x+2 + 2xx2−4...
Divide the sum of 8, 6, 7, 2, 0, 4, 7, 2, 3, by their mean ...
Find the gradient of the line passing through the points P(1, 1) and Q(2, 5). ...
The diagram is a circle with centre O. Find the area of the shaded portion ...