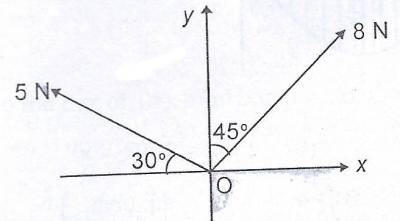
1.7N
4.5N
9.0N
13.0N
Correct answer is A
F = F \cos \theta + F \sin \theta
where F \cos \theta = \text{horizontal component}
F \sin \theta = \text{vertical component}
Horizontal component of resultant = sum of horizontal compoents of individual forces
= 8 \cos 30 + 10 \cos 150 = 6.928 - 8.66 \approxeq - 1.7N
The sum, S_{n}, of a sequence is given by S_{n} = 2n^{2} - 5. Find the 6th term
112
67
45
22
Correct answer is D
S_{n} = 2n^{2} - 5
T_{n} = S_{n} - S_{n - 1}
T_{6} = S_{6} - S_{5}
= (2(6^{2} - 5) - (2(5^{2} - 5) = 62 - 40 = 22
If 2\sin^{2} \theta = 1 + \cos \theta, 0° \leq \theta \leq 90°, find the value of \theta.
90°
60°
45°
30°
Correct answer is B
2\sin^{2} \theta = 1 + \cos \theta
2 ( 1 - \cos^{2} \theta) = 1 + \cos \theta
2 - 2\cos^{2} \theta = 1 + \cos \theta
0 = 1 - 2 + \cos \theta + 2\cos^{2} \theta
2\cos^{2} \theta + \cos \theta - 1 = 0
Factorizing, we have
(\cos \theta + 1)(2\cos \theta - 1) = 0
Note: In the range, 0° \leq \theta \leq 90°, all trig functions are positive, so we consider
2\cos \theta = 1 \implies \cos \theta = \frac{1}{2}
\theta = 60°.
WAEC Subjects
Aptitude Tests