In the diagram, O is the center of the circle QRS and&nbs...
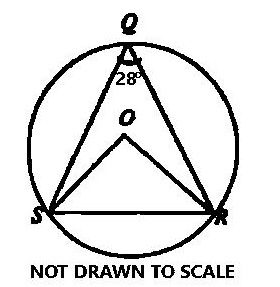
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
\(56^0\)
\(28^0\)
\(76^0\)
\(62^0\)
Correct answer is D
∠SOR = 2 × 28° = 56° (angle at the centre is twice the angle at the circumference)
From ∆SOR
|OS| = |OR| (radii)
So, ∆SOR is isosceles.
∠ORS = \(\frac{180^0 - 56^0}{2} = \frac{124^0}{2}\) ( base angles of isosceles triangle are equal)
∴ ∠ORS = 62°
Similar Questions
Make x the subject of the relation \(\frac{1 + ax}{1 - ax}\) = \(\frac{p}{q}\)...
If the mean of 3, 5, 8, k, 14 and 17 is 11, what is the value of k ...
Solve the inequality: 3m + 3 > 9 ...
Solve the simultaneous equation: x+y=2 and 3x-2y=1 ...
The locus of a point P which is equidistant from two given points S and T is ...