Find the sum to infinity of the series
\(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{16}\),..........
\(\frac{1}{2}\)
\(\frac{3}{5}\)
\(\frac{-1}{5}\)
\(\frac{73}{12}\)
Correct answer is A
Sum to infinity
∑ = arn − 1
= \(\frac{a}{1}\) − r
a = \(\frac{1}{4}\)
r = \(\frac{1}{8}\) ÷ \(\frac{1}{4}\)
r = \(\frac{1}{s}\) × \(\frac{4}{1}\)
= \(\frac{1}{2}\)
S = \(\frac{1 \div 4}{1}\) − \(\frac{1}{2}\)
= \(\frac{1}{4}\) ÷ \(\frac{1}{2}\)
= \(\frac{1}{4}\) × \(\frac{2}{1}\)
= \(\frac{1}{2}\)
16
14
12
10
Correct answer is A
Range = Highest Number - Lowest Number
Mode is the number with highest occurrence
10, 9, 10, 9, 8, 7, 7, 10, 8, 4, 6,, 9, 10, 9, 7, 10, 6, 5
Range = 10 − 4 = 6
Mode = 10
Sum of range and mode = range + mode = 6 + 10
= 16
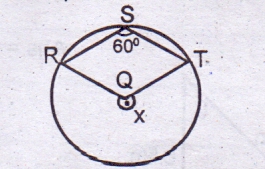
100o
140o
120o
10o
Correct answer is C
If RST = 60o
RXT = 2 × RST
(angle at the centre twice angle at the circumference)
RXT = 2 × 60
= 120o
The locus of a point which is equidistant from the line PQ forms a
circle centre P
pair of parallel lines each opposite to PQ
circle centre Q
perpendicular line to PQ
Correct answer is D
The locus of points at a fixed distance from the point P is a circle with the given P at its centre.
The locus of points at a fixed distance from the point Q is a circle with the given point Q at its centre
The locus of points equidistant from two points P and Q i.e line PQ is the perpendicular bisector of the segment determined by the points
Hence, The locus of a point which is equidistant from the line PQ forms a perpendicular line to PQ
Simplify 3 \(^{n − 1}\) × \(\frac{27^{n + 1}}{81^n}\)
3\(^{2n}\)
9
3n
3 \(^{n + 1}\)
Correct answer is B
3\(^{n - 1}\) × \(\frac{27^{n + 1}}{81^n}\)
= 3\(^{n - 1}\) × \(\frac{3^{3(n + 1)}}{3^{4n}}\)
= 3\(^{n - 1 + 3n + 3 − 4n}\)
= 3\(^{4n − 4n − 1 + 3}\)
= \(3^{2}\)
= 9
JAMB Subjects
Aptitude Tests