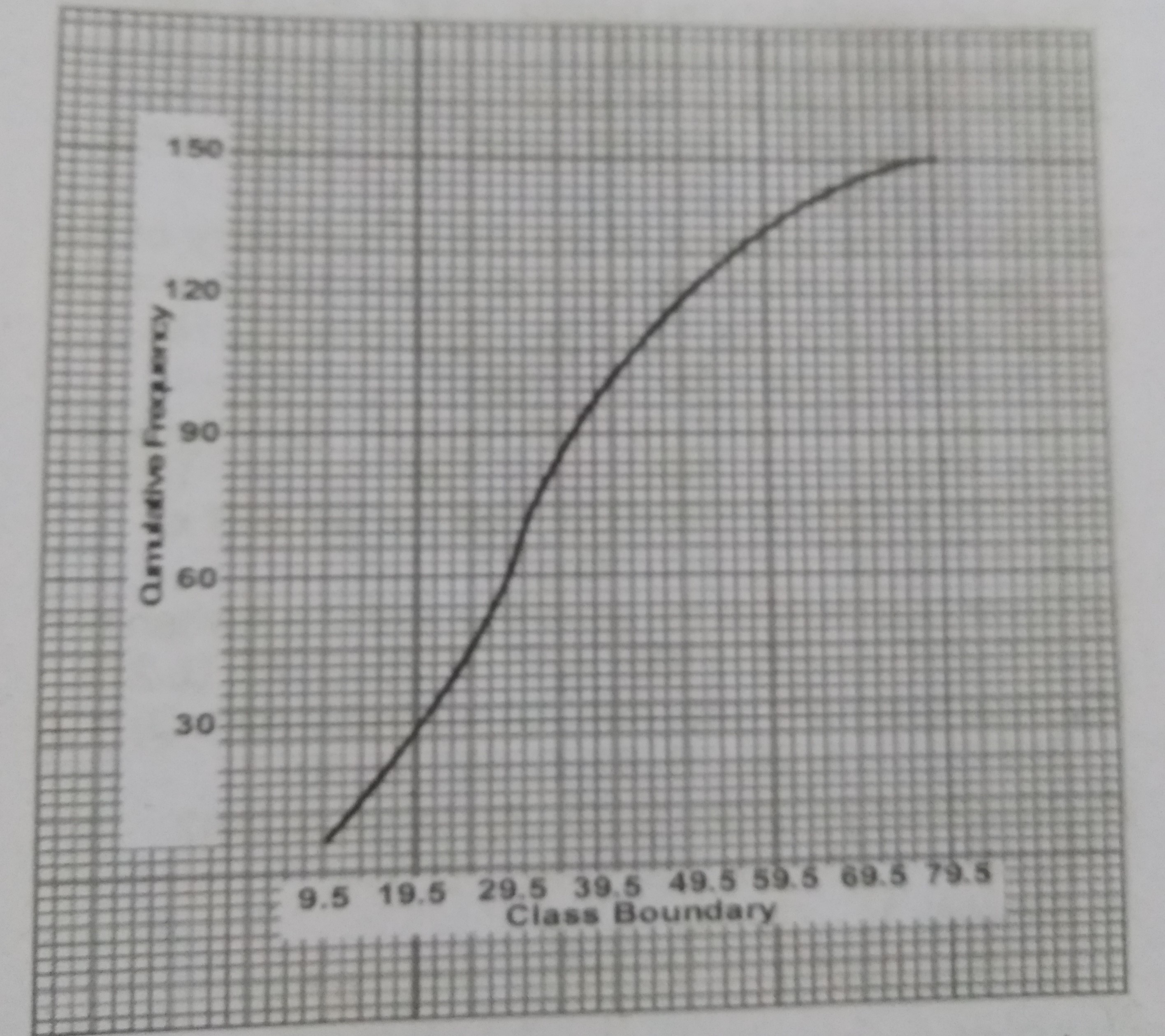
Using the cumulative frequency curve. What is the 80th percentile?
45.5
46.5
47.5
48.5
Correct answer is C
No explanation has been provided for this answer.
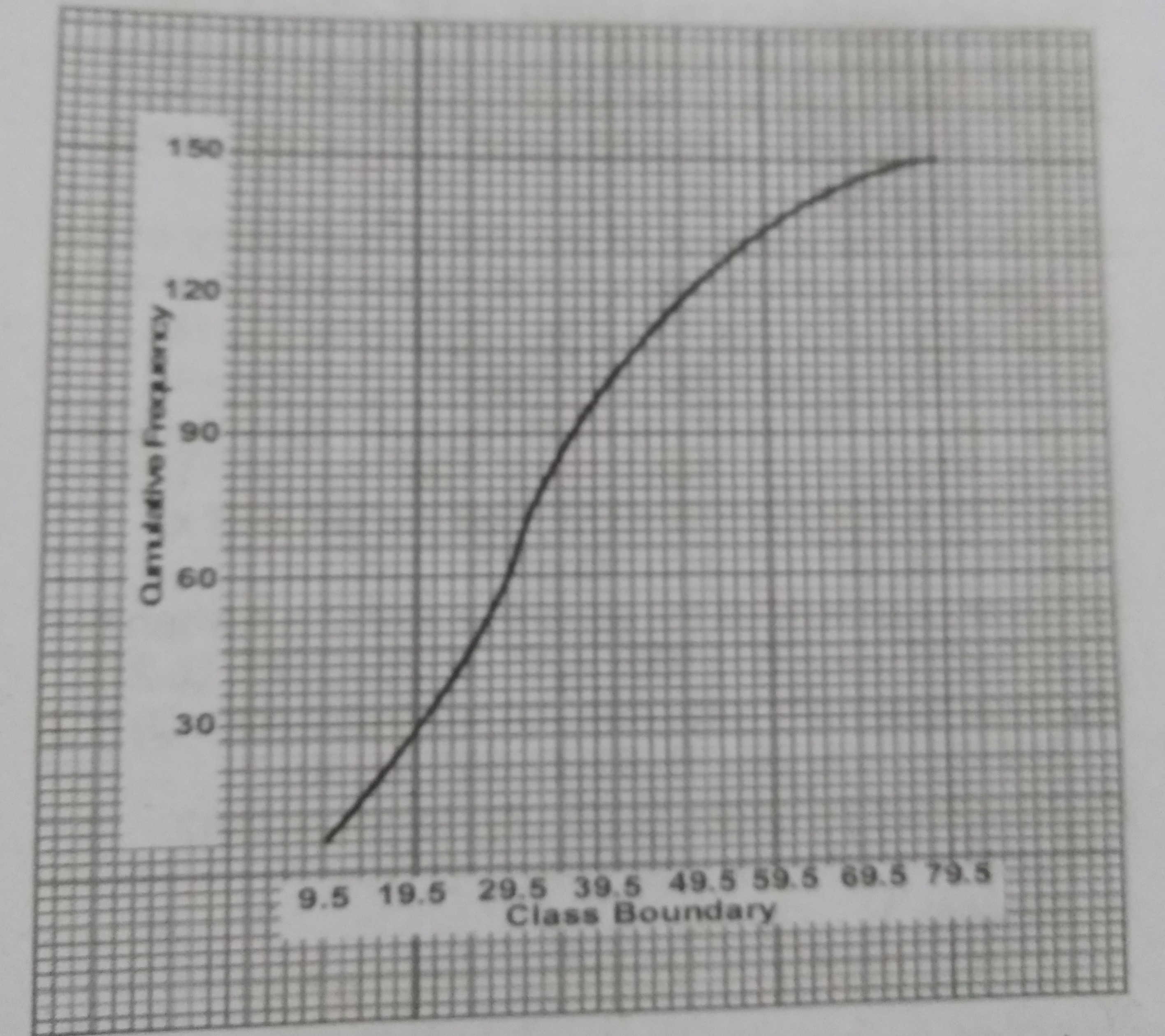
Using the cumulative frequency curve, estimate the median of the data represented on the graph.
35.5
36.5
37.5
38.5
Correct answer is B
No explanation has been provided for this answer.
48 cm
40 cm
43 cm
45 cm
Correct answer is C
Perimeter of the sector = \(2r + \frac{\theta}{360°} \times 2\pi r\)
= \(2(10.5) + \frac{120}{360} \times 2 \times \frac{22}{7} \times 10.5\)
= \(21 + 22\)
= 43 cm
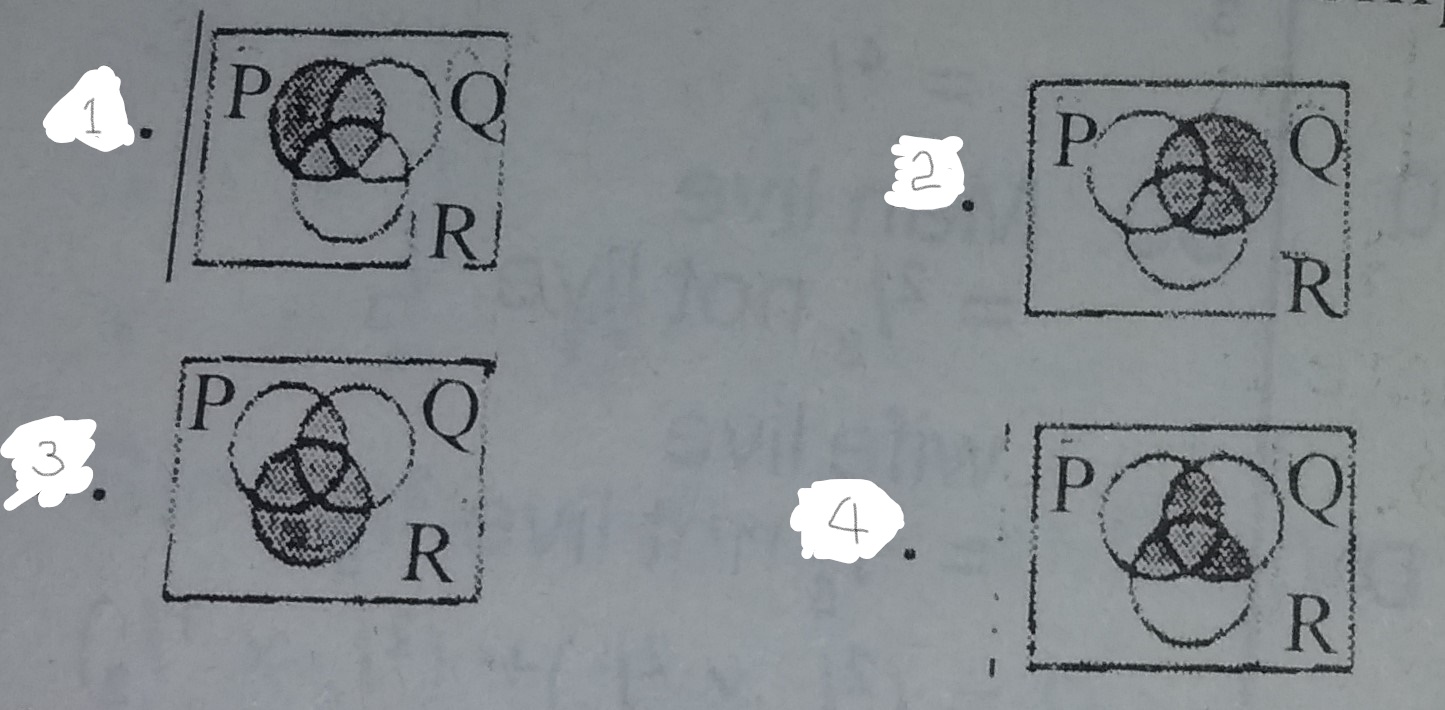
1
2
3
4
Correct answer is C
No explanation has been provided for this answer.
Evaluate \(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\)
-2
2
1
-1
Correct answer is C
\(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\)
= \(- \cos x |_{0} ^{\frac{\pi}{2}\)
= \(- \cos (\frac{\pi}{2}) - (- \cos 0)\)
= \(0 + 1\)
= 1
JAMB Subjects
Aptitude Tests