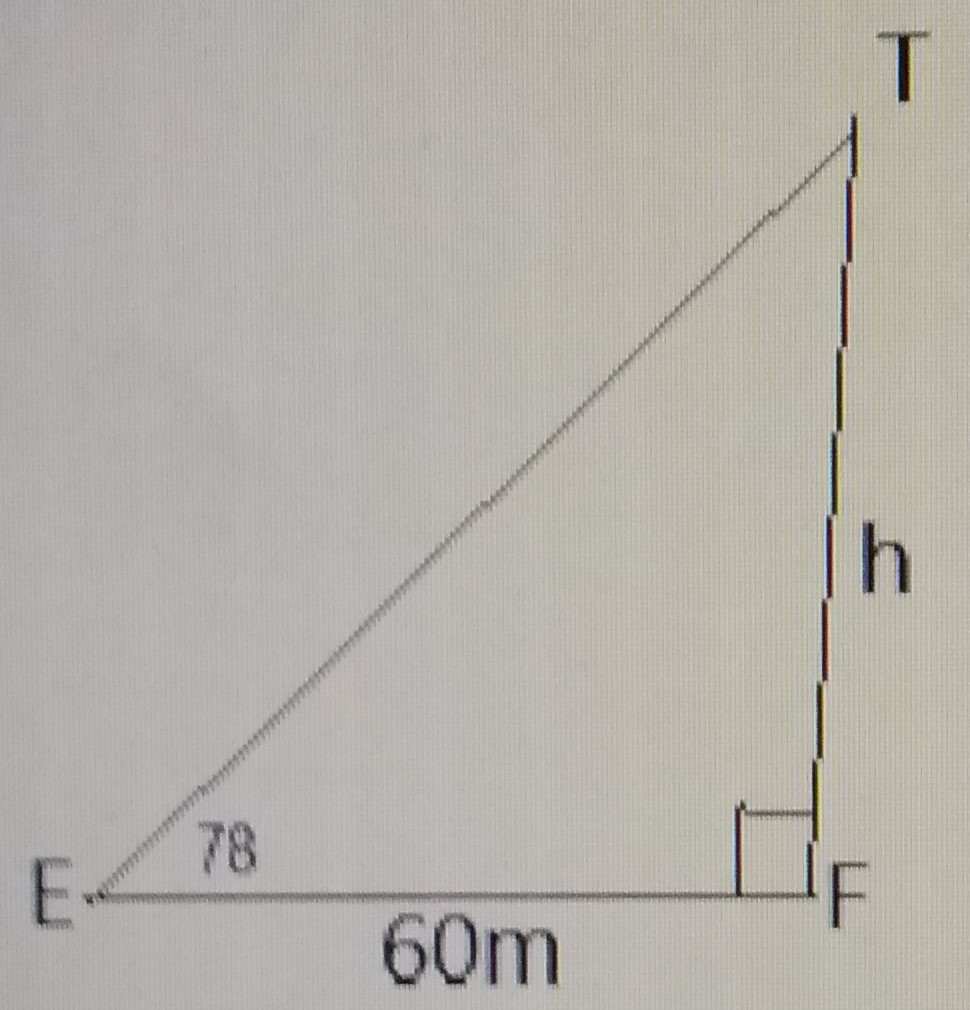
276.
A.
6
B.
25
C.
15
D.
18
Correct answer is C
m⊗n=mn+m−n
3 ⊗ (2 ⊗ 4)
2 ⊗ 4 = 2(4) + 2 - 4 = 6
3 otimes 6 = 3(6) + 3 - 6 = 15
278.
Make q the subject of the formula in the equation \frac{mn}{a^2} - \frac{pq}{b^2} = 1
A.
q = \frac{b^2(mn - a^2)}{a^2 p}
B.
q = \frac{m^2 n - a^2}{p^2}
C.
q = \frac{mn - 2b^2}{a^2}
D.
q = \frac{b^2 (n^2 - ma^2)}{n}
Correct answer is A
\frac{mn}{a^2} - \frac{pq}{b^2} = 1
\frac{mn}{a^2} - 1 = \frac{pq}{b^2}
\frac{mn - a^2}{a^2} = \frac{pq}{b^2}
pq = \frac{b^2 (mn - a^2)}{a^2}
q = \frac{b^2(mn - a^2)}{a^2 p}
JAMB Subjects
Aptitude Tests