| Score (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Freq (f) | 5 | 7 | 3 | 7 | 11 | 6 | 7 |
Find the mean of the data.
3.26
4.91
6.57
3.0
Correct answer is A
Mean = \(\frac{\sum fx}{\sum f}\)
= \(\frac{150}{46}\)
= 3.26
\(\begin{vmatrix} -4 & 2 & 1\\ 6 & 0 & 5 \\ 0 & 6 & 2 \end{vmatrix}\)
\(\begin{vmatrix} -6 & 0 & 13\\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)
\(\begin{vmatrix} 5 & 2 & 6 \\ 0 & 1 & 1\\ 3 & 4 & -7 \end{vmatrix}\)
\(\begin{vmatrix} -4 & 0 & 8 \\ 0 & -2 & -16 \\ 10 & 12 & 6 \end{vmatrix}\)
Correct answer is B
M = \(\begin{vmatrix} -2 & 0 & 4 \\ 0 & -1 & 6 \\ 5 & 6 & 3 \end{vmatrix}\)
M\(^{T}\) = \(\begin{vmatrix} -2 & 0 & 5 \\ 0 & -1 & 6\\ 4 & 6 & 3 \end{vmatrix}\)
2M = \(\begin{vmatrix} -4 & 0 & 8\\ 0 & -2 & 12\\ 10 & 12 & 6\end{vmatrix}\)
M\(^T\) + 2M = \(\begin{vmatrix} -6 & 0 & 13 \\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)
In how many ways can the word MATHEMATICIAN be arranged?
6794800 ways
2664910 ways
6227020800 ways
129729600 ways
Correct answer is D
MATHEMATICIAN = 13 letters with 2M, 3A, 2T, 2I.
Hence, the word MATHEMATICIAN can be arranged in \(\frac{13!}{2! 3! 2! 2!}\)
= 129729600 ways
If a fair coin is tossed 3 times, what is the probability of getting at least two heads?
\(\frac{2}{3}\)
\(\frac{4}{5}\)
\(\frac{2}{5}\)
\(\frac{1}{2}\)
Correct answer is D
The outcomes are {HHH, HHT, HTT, HTH, THH, THT, TTH, TTT}
P(at least two heads) = \(\frac{4}{8}\)
= \(\frac{1}{2}\)
If \(6x^3 + 2x^2 - 5x + 1\) divides \(x^2 - x - 1\), find the remainder.
9x + 9
2x + 6
6x + 8
5x - 3
Correct answer is A
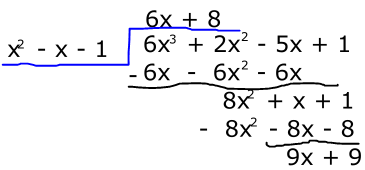
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests