180\(^o\)
36\(^o\)
60\(^o\)
108\(^o\)
Correct answer is B
Total number of acres = 2 + 5 + 3 + 11 + 9 = 30
The angle of acres = 2 + 5 + 3 + 11 + 9 = 30
The angle of the sector for cassava in a pie chart = \(\frac{3}{30} \times 360^o = 36^o\)
25m
23m
22m
20m
Correct answer is D
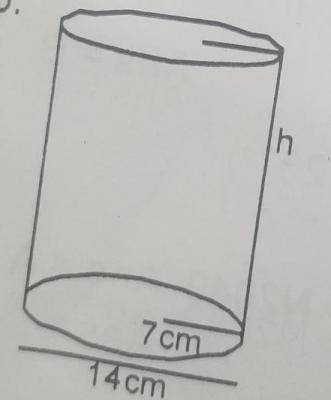
V = 2080cm\(^3\), h = ?
r = 7cm
V = V\(\pi r^2h\)
h = \(\frac{V}{\pi r^2} = \frac{3080}{\frac{22}{7} \times 49}\)
\(\frac{3080}{54}\) = 20cm
8cm
9cm
6cm
7cm
Correct answer is C
No explanation has been provided for this answer.
The chord ST of a circle is equal to the radius r of the circle. Find the length of arc ST
\(\frac{\pi r}{3}\)
\(\frac{\pi r}{2}\)
\(\frac{\pi r}{12}\)
\(\frac{\pi r}{6}\)
Correct answer is A
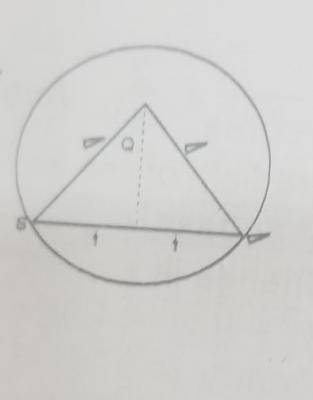
\(\frac{ \frac{r}{2}}{r}\) Sin \(\theta\) = \(\frac{1}{2}\)
\(\theta\) = sin\(^{-1}\) (\(\frac{1}{2}\)) = 30\(^o\) = 60\(^o\)
Length of arc (minor)
ST = \(\frac{\theta}{360}\) x 2\(\pi r\)
\(\frac{60}{360} \times 2 \pi \times r = \frac{\pi}{3}\)
A binary operation x is defined by a x b = a\(^b\). If a x 2 = 2 - a, find the possible values of a?
1, -2
2, -1
2, -2
1, -1
Correct answer is A
a = b = a\(^2\)
a + 2 = a\(^2\).....(i)
a + 2 = 2 - a..............(ii)
a\(^2\) = 2 - a
a\(^2\)+ a - 2 = a\(^2\) + a - 2 = 0
= (a + 2)(a - 1) = 0
a = 1 or - 2
JAMB Subjects
Aptitude Tests