The chord ST of a circle is equal to the radius r of the ...
The chord ST of a circle is equal to the radius r of the circle. Find the length of arc ST
\(\frac{\pi r}{3}\)
\(\frac{\pi r}{2}\)
\(\frac{\pi r}{12}\)
\(\frac{\pi r}{6}\)
Correct answer is A
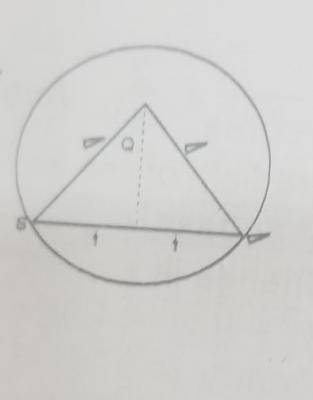
\(\frac{ \frac{r}{2}}{r}\) Sin \(\theta\) = \(\frac{1}{2}\)
\(\theta\) = sin\(^{-1}\) (\(\frac{1}{2}\)) = 30\(^o\) = 60\(^o\)
Length of arc (minor)
ST = \(\frac{\theta}{360}\) x 2\(\pi r\)
\(\frac{60}{360} \times 2 \pi \times r = \frac{\pi}{3}\)
Similar Questions
Which of the following is/are not the interior angle(s) of a regular polygon? I.108° I...
Tom will be 25 years old in n years' time. If he is 5 years younger than Bade's present age....
In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS ...
Given that n(p) = 19, m(P \(\cup\) Q) = 38 and n(P \(\cap\) Q) = 7, Find n(C) ...
One of the following statements is wrong. Which is it? ...
The figure is a solid with the trapezium PQRS as its uniform cross-section. Find its volume ...
A girl walks 45 meters in the direction 050o from a point Q to a point X. She then walks 24 met...