Correct 241.34(3 x 10\(^{-3}\))\(^2\) to 4 significant figures
0.0014
0.001448
0.0022
0.002172
Correct answer is D
first work out the expression and then correct the answer to 4 s.f = 241.34..............(A)
(3 x 10-\(^3\))\(^2\)............(B)
= 3\(^2\)x\(^2\)
= \(\frac{1}{10^3}\) x \(\frac{1}{10^3}\)
(Note that x\(^2\) = \(\frac{1}{x^3}\))
= 24.34 x 3\(^2\) x \(\frac{1}{10^6}\)
= \(\frac{2172.06}{10^6}\)
= 0.00217206
= 0.002172(4 s.f)
Find the derivative of the function y = 2x\(^2\)(2x - 1) at the point x = -1?
18
16
-4
-6
Correct answer is B
y = 2x\(^2\)(2x - 1)
y = 4x\(^3\) - 2x\(^2\)
dy/dx = 12x\(^2\) - 4x
at x = -1
dy/dx = 12(-1)\(^2\) - 4(-1)
= 12 + 4
= 16
234.00 cm3
526.50 cm3
166.00 cm3
687cm3
Correct answer is A
Let x represent total vol. 2 : 3 = 2 + 3 = 5
\(\frac{3}{5}\)x = 351
x = \(\frac{351 \times 5}{3}\)
= 585
Volume of smaller block = \(\frac{2}{5}\) x 585
= 234.00cm\(^3\)
\(\frac{-2}{7}\)
\(\frac{7}{6}\)
\(\frac{-6}{7}\)
2
Correct answer is D
Line: 2y+8x-17=0
recall y = mx + c
2y = -8x + 17
y = -4x + \(\frac{17}{2}\)
Slope m\(_1\) = 4
parallel lines: m\(_1\). m\(_2\) = -4
where Slope ( -4) = \(\frac{y_2 - y_1}{x_2 - x_1}\) at points (-1, -p) and (-2,2)
-4( \(x_2 - x_1\) ) = \(y_2 - y_1\)
-4 ( -2 - -1) = 2 - -p
p = 4 - 2 = 2
13 cm
4 cm
6 cm
7 cm
Correct answer is A
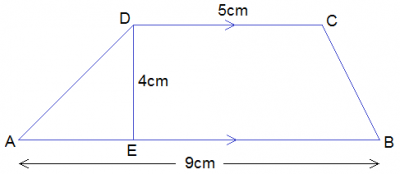
Area of Trapezium = 1/2(sum of parallel sides) * h
91 = \(\frac{1}{2}\) (5 + 9)h
cross multiply
91 = 7h
h = \(\frac{91}{7}\)
h = 13cm
JAMB Subjects
Aptitude Tests