\(\frac{5}{9}\)k2 sq. units
\(\frac{1}{3}\)k2 sq. units
\(\frac{8}{9}\)k2 sq. units
\(\frac{7}{9}\)k2 sq. units
\(\frac{2}{3}\)k2 sq. u
Correct answer is A
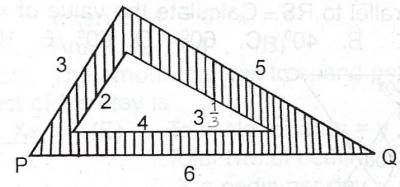
Area of shaded portion = Area of triangle PQR - Area of inner triangle
Area of triangle given 3 sides a, b, c = \(\sqrt{s(s - a)(s - b)(s - c)}\)
where \(s = \frac{a + b + c}{2} \)
Area of PQR :
\(s = \frac{3 + 5 + 6}{2} = \frac{14}{2} = 7\)
Area = \(\sqrt{7(7 - 3)(7 - 5)(7 - 6)}\)
= \(\sqrt{7(4)(2)(1)} = \sqrt{56}\)
\(\implies K^{2} = \sqrt{56}\)
Area of inner triangle :
\(s = \frac{2 + 4 + \frac{10}{3}}{2} = \frac{14}{3}\)
Area = \(\sqrt{\frac{14}{3} (\frac{14}{3} - 2)(\frac{14}{3} - 4)(\frac{14}{3} - \frac{10}{3})}\)
= \(\sqrt{\frac{14}{3} (\frac{8}{3})(\frac{2}{3})(\frac{4}{3})}\)
= \(\sqrt{\frac{896}{81}}\)
= \(\sqrt{\frac{16}{81}} \times \sqrt{56}\)
= \(\frac{4}{9} K^{2}\)
\(\therefore \text{The area of the shaded portion} = K^{2} - \frac{4}{9}K^{2} = \frac{5}{9}K^{2}\)
45o
35o
40o
30o
42o
Correct answer is D
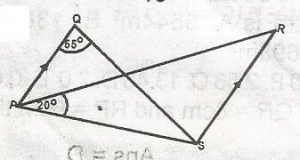
PSR = 65o x 2
= 130o
PRS = 180o - (130o + 20o)
= 30o
70o
90o
80o
40o
60o
Correct answer is C
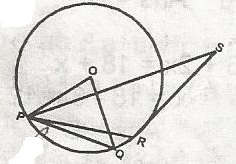
Isosceles Triangle PSR:
RSP ≡ RPS → 20º
That is PRQ = 40º
POQ = 2 * 40 = 80º (Angle subtended by chord PQ at centre is twice angle subtended at circumference).
The size of POQ = 80º
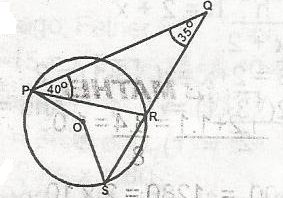
If O is the centre of the circle, < POS equls
70o
75o
105o
140o
150o
Correct answer is E
Since O is the centre of the circle < POS = 150o
i.e. < substended at the centre is twice that substended at any part of the circumference
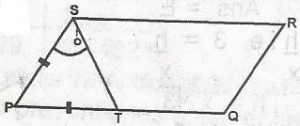
In this figure, PQRS is a parallelogram, PS = PT and < PST = 55\(^o\). The size of <PQR is
125o
120o
115o
110o
10o
Correct answer is D
Both pairs of opp. angles are equal
< STP = 55\(^o\) - isosceles angle
< TSR = 55\(^o\) - alternate angle to < STP
Hence, < PSR = 55\(^o\) + 55\(^o\) = 110\(^o\)
\(\therefore\) < PQR = 110\(^o\)
JAMB Subjects
Aptitude Tests