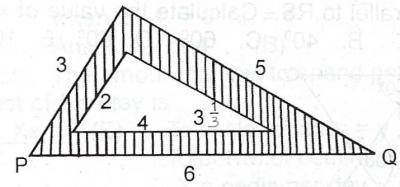
(Numbers indicate the lengths of the sides of the triangles) If the area of \(\bigtriangleup\) PQR is k2sq. units what is the area of the shades portion?
\(\frac{5}{9}\)k2 sq. units
\(\frac{1}{3}\)k2 sq. units
\(\frac{8}{9}\)k2 sq. units
\(\frac{7}{9}\)k2 sq. units
\(\frac{2}{3}\)k2 sq. u
Correct answer is A
Area of shaded portion = Area of triangle PQR - Area of inner triangle
Area of triangle given 3 sides a, b, c = \(\sqrt{s(s - a)(s - b)(s - c)}\)
where \(s = \frac{a + b + c}{2} \)
Area of PQR :
\(s = \frac{3 + 5 + 6}{2} = \frac{14}{2} = 7\)
Area = \(\sqrt{7(7 - 3)(7 - 5)(7 - 6)}\)
= \(\sqrt{7(4)(2)(1)} = \sqrt{56}\)
\(\implies K^{2} = \sqrt{56}\)
Area of inner triangle :
\(s = \frac{2 + 4 + \frac{10}{3}}{2} = \frac{14}{3}\)
Area = \(\sqrt{\frac{14}{3} (\frac{14}{3} - 2)(\frac{14}{3} - 4)(\frac{14}{3} - \frac{10}{3})}\)
= \(\sqrt{\frac{14}{3} (\frac{8}{3})(\frac{2}{3})(\frac{4}{3})}\)
= \(\sqrt{\frac{896}{81}}\)
= \(\sqrt{\frac{16}{81}} \times \sqrt{56}\)
= \(\frac{4}{9} K^{2}\)
\(\therefore \text{The area of the shaded portion} = K^{2} - \frac{4}{9}K^{2} = \frac{5}{9}K^{2}\)
Similar Questions
If 23\(_y\) = 1111\(_{\text{two}}\), find the value of y...
Simplify \(\frac{5+\sqrt{7}}{3+\sqrt{7}}\) ...
If \(3x - \frac{1}{4})^{\frac{1}{2}} > \frac{1}{4} - x \), then the interval of values of x ...
Evaluate \(log_{10}5 + log_{10}20\)...
The remainder when 6p3 - p2 - 47p + 30 is divided by p - 3 is...
In the diagram, O is the centre of the circle of radius 18cm. If < zxy = 70\(^o\), calculate the ...