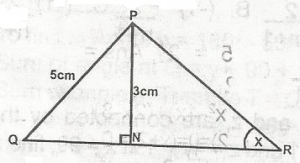
If PN is perpendicular to QR, find the value of tan x.
\(\frac{5}{9}\)
\(\frac{3}{5}\)
\(\frac{3}{4}\)
\(\frac{4}{3}\)
\(\frac{4}{3}\)
Correct answer is B
By Pythagoras ON = 4
NR = 5
Tan x = \(\frac{3}{5}\)
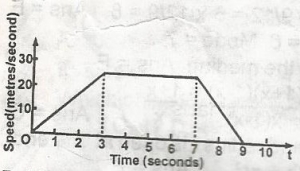
17.72 meter/sec.
21.67 meters/sec
2.5 meter/sec.
20.45 meters/sec.
13.33 meter/sec.
Correct answer is D
Time(sec) areas of the three sides are \(\frac{1}{2}\) x 2 x 20 = 20 x 2 = 40
\(\frac{1}{2}\) x 4 x 20 = 40
40 + 40 = 80
vel. = \(\frac{80}{4}\)
20 + 0.45 = 20.45 meter/sec.
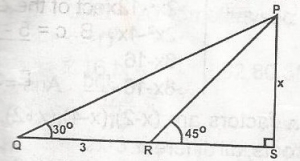
3\(\sqrt{3}\)
\(\frac{3(\sqrt{3} - 1)}{\sqrt{3} + 1}\)
\(\frac{(\sqrt{3} - 1)}{\sqrt{3} + 1}\)
\(\frac{3 - 1}{\sqrt{3} + 1}\)
Correct answer is B
\(\frac{x + 3}{sin 60^o}\) = \(\frac{x}{sin 306o}\)
3sin 30o = x sin 60o - x sin 30o
= x(sin 60o - sin 30o)
but sin 30o = \(\frac{1}{2}\)
sin 60o = \(\frac{3}{2}\) = \(\frac{3(\sqrt{3} - 1)}{\sqrt{3} + 1}\)
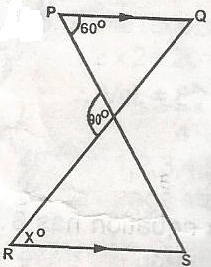
PQ is parallel to RS. Calculate the value of x.
20o
40o
60o
80o
100o
Correct answer is B
< D = 180o - 100v
= 80o (< on a str. line)
< s = 60o - alternate angle
x = 180o - (80o + 60o)
180o - 140o = 40o
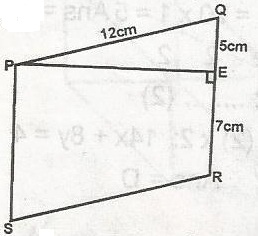
In the parallelogram PQRS, PE is perpendicular to QR. Find the area of the parallelogram.
60cm2
65cm2
72cm2
132cm2
156cm2
Correct answer is D
By Pythagoras, PE\(^2\) = 12\(^2\) - 5\(^2\)
= 144 - 25 = 119
h = PE\(^2\) = √119 = 10.9 ≈ 11cm,
Area of 11gm = b x h
QR = b =(5 + 7)cm = 12cm
area = 12 x 11
= 132cm\(^2\)
JAMB Subjects
Aptitude Tests