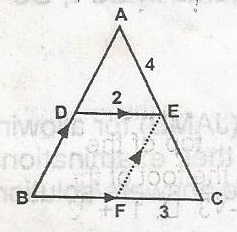
In the figure, DE//BC: DB//FE: DE = 2cm, FC = 3cm, AE = 4cm. Determine the length of EC.
4cm
6cm
3cm
2cm
1cm
Correct answer is B
Angles ADE and EFC are similar,
Therefore,
= x3=42
= x3=2
x = 3 x 2 = 6
387
493
502
441
634
Correct answer is C
Possible multiples of 8 and 9 = 72, 144, 216, 288, 360, 432, 576, 648.
3878 has remainder = 3; 3879 has remainder 0.
4938 has remainder 5; 4939 has remainder 7.
5028 has remainder 6; 5029 has remainder 7.
4418 has remainder 1; 4419 has remainder 0.
6348 has remainder 2; 6349 has remainder 4.
Hence 502 is the answer.
13
14
15
12
11
Correct answer is D
No explanation has been provided for this answer.
2
4
√10
35
2.2
Correct answer is C
a = 2i - 3j - 3i + 6j
= -i + 3j
= √5×2
= √10
3 + √3
5 + √3
3 - √3
1
√3 - 1
Correct answer is D
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests