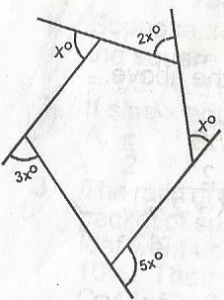
The angles marked in the figure are measured in degrees. Find x.
45o
90o
60o
15o
30o
Correct answer is E
Sum of external angles = 360o
3x + 5x + x + 2x + x = 360o
12x = 360o
x = 30o
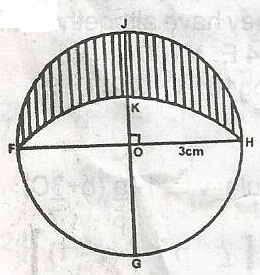
3\(\pi\)\(\sqrt{2 - 1}\)cm
\(\frac{9}{2}\)\(\pi\)cm
3 \(\pi\)(1 + \(\frac{2}{2}\))
3(1 + \(\frac{2}{2}\))
Correct answer is C
Perimeter of lunar portion = 3\(\pi\) + \(\frac{3\pi \sqrt{2}}{2}\)
= 3 \(\pi\)(1 + \(\frac{2}{2}\))
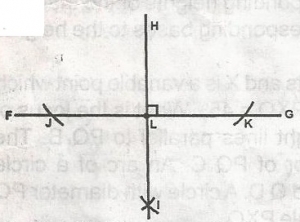
perpendicular bisector of the line
perpendicular bisector of th eline JK
perpendicular bisector of the line HI
perpendicular from H to the line FG
Correct answer is D
No explanation has been provided for this answer.
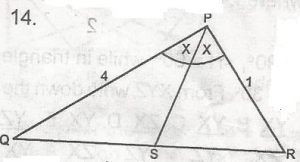
In the figure, PS bisects angle QPR. Find the ratio SR:QR.
1:2
1:3
1:4
1:5
1:6
Correct answer is C
From Internal bisection theorem, \(\frac{QP}{PR}\) = \(\frac{QS}{SR}\)
= \(\frac{4}{1}\)
= 1:4
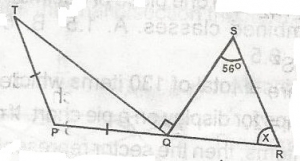
In the figure, If PT is parallel to RS, PQ = PT, and angle SQT = 90o, Find x
35o
50o
55o
70o
80o
Correct answer is D
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests