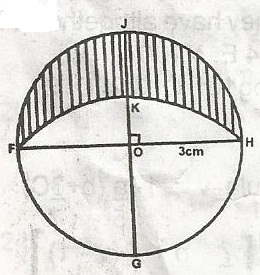
In the figure, FGHJ is a circle of radius 3cm centre O. FOH, GOJ are perpendicular diameters. With G as centre of an arc of a circle is drawn to pass through F and H. Find the length of the perimeter of the lunar portion shaded.

Similar Questions

Evaluate 1 - ($\frac{1}{5}$ x $\frac{2}{3}$) + ( 5 + $\frac{2}{3}$)...

Find the square root of 170 - 20$\sqrt{30}$...

In the diagram above, TPS is a straight line, PQRS is a parallelogram with base QR and height 8...

In the figure, determine the angle marked y ...

\(\begin{array}{c|c} \text{Class Interval} & Frequency & \text{Class boundaries} & Class Mid-point \...

In the diagram, PQ is a straight line. Calculate the value of the angle labelled 2y ...

The weight of 10 pupils in a class are 15 kg, 16 kg, 17 kg, 18 kg, 16 kg, 17 kg, 17 kg, 17 kg, 18 kg...

The angle between latitudes 30oS and 13oN is...

Simplify 3 log69 + log612 + log664 - log672...

PQRS is a desk of dimensions 2m x 0.8 which is inclined at 30o to the horizontal. Find the inclinati...