Loading [MathJax]/jax/output/HTML-CSS/jax.js

JAMB Mathematics Past Questions & Answers - Page 136

676.

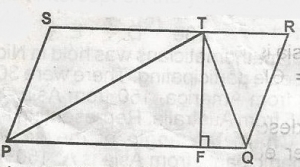
TP and TQ are tangents to a circle centre 0 and r is a point on the circumference of the circle as shown in the figure. If angle PTQ = 45o, what is the magnitude of the angle PRO?

135

76 $\frac{1}{2}$

52 $\frac{1}{2}$

View answer & explanation

Correct answer is D

PTQ = 45^o

< PRQ = 76 $\frac{1}{2}$

677.

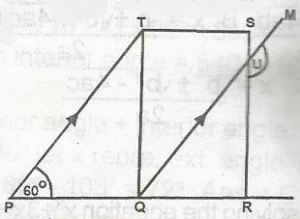
In the figure, QRST is a rectangle; PT// QM, angle P = 60o. Find angle MUR

150^o

30^o

60^o

120^o

90^o

View answer & explanation

Correct answer is A

QRST is a rectangle

PT //QM, P = 60o = angle MUR = 150o

678.

PQRS is a parallelogram with area 50 square cm and the side PQ is 10cm long. T is a point on RS and TF is the altitude of the triangle TPQ. Find TF

10cm

12.5cm

8cm

6cm

5cm

View answer & explanation

Correct answer is E

Area of a //gm PQRS = B X H Area of a //gm PQRS = PQ x TF 50 = 10TF TF = 5cm

679.

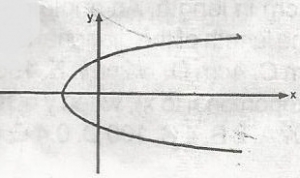
If K is a constant, which of the following equations best describes the parabola?

y = kx²

x = y² - k

y = k - x²

x² = y² - k

y = (k - x)²

View answer & explanation

Correct answer is B

The parabola is best described by the equation x = y² - k because all other equations do not give the equation of the parabola in this position. C for example is the equation of a hyperbola facing downwards. D is the equation of a hyperbola A and E are equations of parabola facing upwards

680.

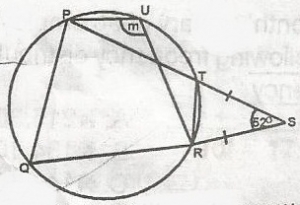
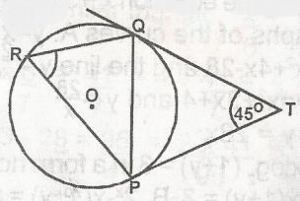
In the fiqure where PQRTU is a circle, ISTI = IRSI and angle TSR = 52^o. Find the angle marked m

128^o

52^o

104^o

64^o

116^o

View answer & explanation

Correct answer is E

< STR = $\frac{180 - 52}{2}$ = $\frac{128}{2}$ = 64^o

< PTR = 180 - < STR(angle on a straight line)

= 180 - 64 = 116^o

< PQR + < PTR = 180(Supplementary)

< PQR + 118 = 180

< PQR = 180 - 118

= 64

M = 180 - < PQR

= 180 - < PQR = 180 - 64

= 116^o