In the fiqure where PQRTU is a circle, ISTI = IRSI and angle...
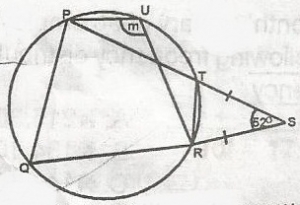
In the fiqure where PQRTU is a circle, ISTI = IRSI and angle TSR = 52o. Find the angle marked m
A.
128o
B.
52o
C.
104o
D.
64o
E.
116o
Correct answer is E
< STR = 180−522 = 1282 = 64o
< PTR = 180 - < STR(angle on a straight line)
= 180 - 64 = 116o
< PQR + < PTR = 180(Supplementary)
< PQR + 118 = 180
< PQR = 180 - 118
= 64
M = 180 - < PQR
= 180 - < PQR = 180 - 64
= 116o
Similar Questions
In the diagram, /TP/ = 12cm and it is 6cm from O, the centre of the circle, Calculate < TOP ...
Given that 3√42x = 16, find the value of x ...
Find the size of each exterior angle of a regular octagon ...
A student sitting on a tower 68 metres high observes his principal's car at the angle of depress...
In the diagram, /MN/, /OP/, /QOP/ = 125o. What is the size of < MQR? ...