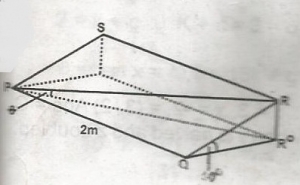
30o 35'
30o 32'
15o 36'
10o
10o 42'
Correct answer is E
tan\(\theta\) = \(\frac{0.8}{2}\) = (0.4)
\(\theta\) = tan-1(0.4)
From the diagram, the inclination of the diagonal PR to the horizontal is 10o 42'
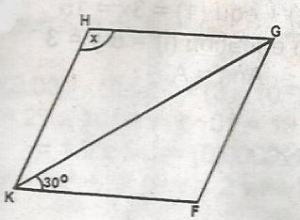
The figure FGHK is a rhombus. What is the value of angle X?
30o
90o
150o
120o
60o
Correct answer is D
< HKF = 60o, < KFG = 120o
< KFG = < KHG = x(opposite angles)
x = 120o
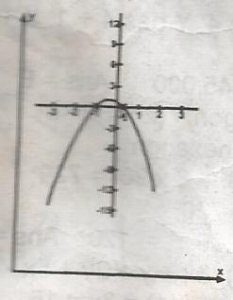
Which of the following equations represents the graph?
y = 1 + 2x + 3x2
y = 1 - 2x + 3x2
y = 1 + 2x - 3x2
y = 1 - 2x - 3x2
y = 3x2 + 2x - 1
Correct answer is E
The roots of the function are 1 and \(\frac{1}{3}\)
sum of roots = -1 + \(\frac{1}{3}\) = -\(\frac{2}{3}\)
product of roots = -1 x \(\frac{1}{3}\) = -\(\frac{1}{3}\)
x2 - (sum of roots)x + (product of roots) = 0
x2 + (-\(\frac{2}{3}\))x - (-\(\frac{1}{3}\)) = 0
x2 + \(\frac{2x}{3}\) - \(\frac{1}{3}\) = 0
3x2 + 2x - 1 = 0
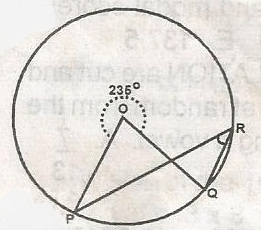
66\(\frac{1}{2}\)o
62\(\frac{1}{2}\)o
125o
105o
65o
Correct answer is B
Angle subtended at any part of the circumference of the circle \(\frac{125^o}{2}\) at centre = 360o - 235o = 125o
\(\bar{PQR}\) = \(\frac{125}{2}\)
= 62\(\frac{1}{2}\)o
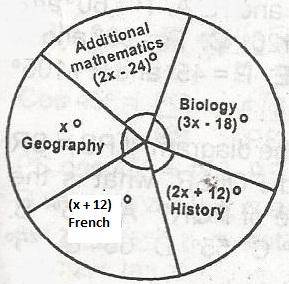
15
10
18
12
20
Correct answer is B
(2x - 24)° + (3x - 18)° + (2x + 12)° + (x + 12)° + x° = 360°
9x = 360° + 18°
x = \(\frac{378}{9}\)
= 42°, if x = 42°, then add maths = \(\frac{2x - 42}{360}\) x 60
= \(\frac{2 \times 42 - 24}{360}\) x 60
= \(\frac{84 - 24}{6}\)
JAMB Subjects
Aptitude Tests