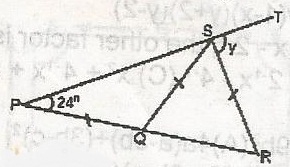
If PST is a straight line and PQ = QS = SR in the diagram, find y.
24o
48o
72o
84o
Correct answer is A
< PSQ = < SQR = < SRQ = 24o
< QSR = 180o - 48o = 132o
< PSQ + < QSR + y + 180 (angle on a straight lines)
24 + 132 + y = 180o = 156o + y = 180
y = 180o - 156o
= 24o
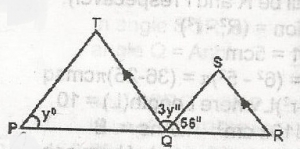
If PQR is a straight line with QS = QR, calculate TPQ, If QT\\SR and TQS = 3yo
62o
56\(\frac{3}{2}\)o
20\(\frac{3}{2}\)o
18o
Correct answer is C
Since QS = QR
then, angle SQR = angle SRQ
2 SQR = 180 - 56, SQR = \(\frac{124}{2}\) = 62o
QTP = 62o
QTP = 62o, corresponding angle
3y + 56 + 62 = 180 = 3y = 180 - 118
3y = 62 = 180
3y = 180 - 118
3y = 62
y = \(\frac{62}{3}\)
= 20\(\frac{3}{2}\)
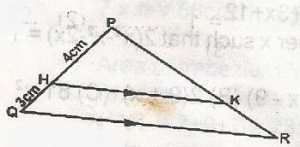
In the diagram, HK is parallel to QR, PH = 4cm and HQ = 3cm. What is the ratio of KR:PR?
7:3
3:7
3:4
4:3
Correct answer is B
In \(\bigtriangleup\)PHK and \(\bigtriangleup\)PAR = \(\frac{PH}{PQ} = \frac{PK}{PR}\)
\(\frac{4}{7} \times \frac{PR-KR}{PR}\)
4PR = 7(PR - KR) = 7PR - 7KR
\(\frac{KR}{PR} = \frac{3}{7}\)
KR:PR = 3:7
120o
110o
60o
20o
Correct answer is D
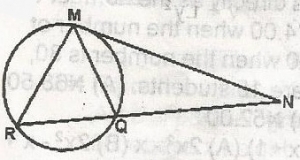
QMN = 60o
MRQ = 60o(angle in the alternate segment are equal)
MQN = 80o(angle sum of a \(\bigtriangleup\) = 180o)
60 = x = 80o(exterior angle = sum of opposite interior angles)
x = 80o - 60o = 20o
RMQ = 20o
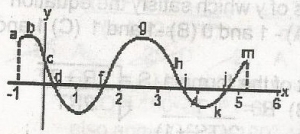
On the curve, the points at which the gradient of the curve is equal to zero are
c, d, f. i, l
b, e, g, j, m
a, b, c, d, f, i, j, l
c, d, f, h, i, l
Correct answer is B
The gradient of any curve is equal to zero at the turning points. i.e. maximum or minimum points. The points in the above curve are b, e, g, j, m
JAMB Subjects
Aptitude Tests