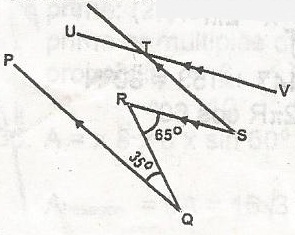
In the figure, PQ||ST, RS||UV. If PQR = 35o and QRS = 65o, find STV
30o
35o
55o
65o
Correct answer is A
Draw XW//PQ and ARW = 35o (alternative angle)
WRS = 60 - 30
= 30o
RSR = 30o (Alternative angle)
STV = 30o (Alternative angle)
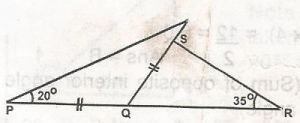
20o
55o
75o
140o
Correct answer is C
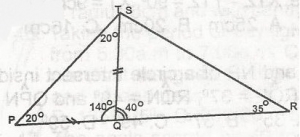
Given △ isosceles PQ = QT, SRQ = 35o
TPQ = 20o
PQR = is a straight line
Since PQ = QT, angle P = angle T = 20o
Angle PQR = 180o - (20 + 20) = 140o
TQR = 180o - 140o = 40o < on a straight line
QSR = 180o - (40 + 35)o = 105o
TSR = 180o - 105o
= 75o
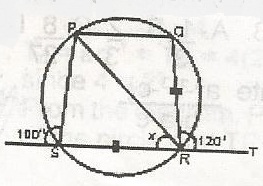
In the figure, PQRS is a circle. If chords QR and RS are equal, calculate the value of x
80o
60o
45o
40o
Correct answer is D
SRT is a straight line, where QRT = 120
SRQ = 180o - 120o = 60o - (angle on a straight line)
also angle QRS = 180o - 100o (angle on a straight line) . In angles where QR = SR and angle SRQ = 60o
x = 100 - 60 = 40o
34o
56o
68o
112o
Correct answer is C
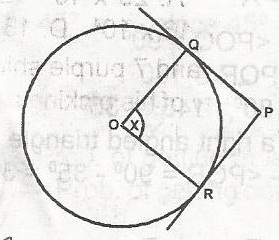
From the circle centre 0, if PQ & PR are tangents from P and QRP = 34o
Then the angle marked x i.e. QOP
34o x 2 = 68o
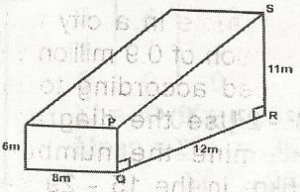
The figure is a solid with the trapezium PQRS as its uniform cross-section. Find its volume
120m2
576m3
816m3
1056m3
Correct answer is C
Volume of solid = cross section x H
Since the cross section is a trapezium
= 12(6+11)×12×8
= 6 x 17 x 8 = 816m3
JAMB Subjects
Aptitude Tests