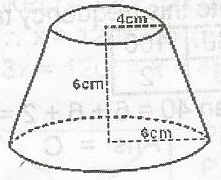
Find the curved surface area of the frustrum in the figure
16\(\pi \sqrt{10}\)cm2
20\(\pi \sqrt{10}\)cm2
24\(\pi \sqrt{10}\)cm2
36\(\pi \sqrt{10}\)cm2
Correct answer is B
\(\frac{x}{4} = \frac{6 + x}{6}\)
6x = 4(6 + x) = 24 + 4x
x = 12cm
CSA = \(\pi RL - \pi rl\)
= \(\pi (6) \sqrt{{18^2} + 6^2} - \pi \times 4 \times \sqrt{{12^2} + 4^2}\)
= 6\(\pi \sqrt{360} - 4 \pi \sqrt{160}\)
= 36\(\pi \sqrt{10} - 16 \pi \sqrt{10}\)
= 20\(\pi \sqrt{10}\)cm2
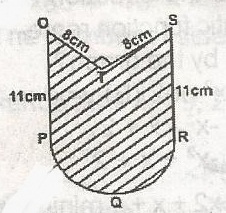
In the figure, PQR is a semicircle. Calculate the area of the shaded region
125\(\frac{2}{7}\)2
149\(\frac{2}{7}\)cm2
234\(\frac{1}{7}\)cm2
267\(\frac{1}{2}\)cm2
Correct answer is A
No explanation has been provided for this answer.
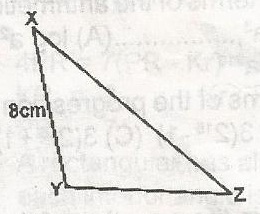
In the figure, YXZ = 30o, XYZ = 105o and XY = 8cm. Calculate YZ
16\(\sqrt{2}\)cm
8\(\sqrt{2}\)cm
4\(\sqrt{2}\)cm
22cm
Correct answer is C
yzx + 105o + 30o = 180o
yzx = 180 - 155 = 45o
\(\frac{yz}{sin 30^o} = \frac{8}{sin 45^o}\)
yz = \(\frac{8 \sin 30}{sin 45}\)
= 8(\(\frac{1}{2}) = \frac{8}{1} \times \frac{1}{2} \times \frac{\sqrt{2}}{1}\)
= 4 \(\div\) \(\frac{1}{\sqrt{2}}\)
= 4\(\sqrt{2}\)cm
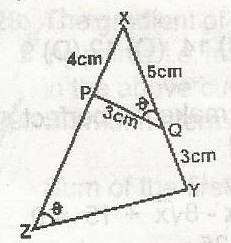
In triangles XYZ and XQP, XP = 4cm, XQ = 5cm and PQ = QY = 3cm. Find ZY
8cm
6cm
4cm
3cm
Correct answer is B
No explanation has been provided for this answer.
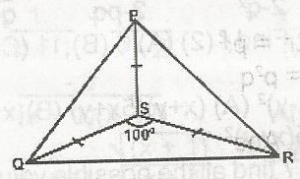
In the figure, PS = QS = RS and QSR - 100o, find QPR
40o
50o
80o
100o
Correct answer is B
Since PS = QS = RS
S is the centre of circle passing through P, Q, R /PS/ = /RS/ = radius
QPR \(\pm\) \(\frac{100^o}{2}\) = 50o
JAMB Subjects
Aptitude Tests