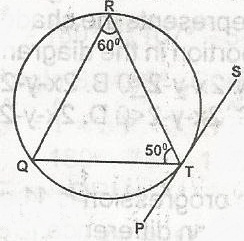
In the diagram, PTS is a tangent to the circle TQR at T. Calculate < RTS
120o
70o
60o
40o
Correct answer is B
RTS = RQT (angle between a tangent and a chord at the point of contact is equal to the angle in the alternate segment) But R = Q + T = 180
RQT = 180o - (50 + 60)
= 180o - 110o
= 70o
Since RQT = RTS = 70o
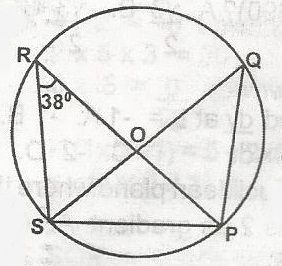
148o
104o
80o
52o
Correct answer is D
< SRP = < SQP = 38o (angle in the same segment of a circle are equal)
But < SPQ = 90o (angle in a semicircle)
also < PSQ + < SQP + < SPQ = 180o (angles in a triangle = 180o)
< PSQ + 38o + 90o = 190o
< PSQ = 128o = 180o
PSQ = 180o - 128o
PSQ = 52o
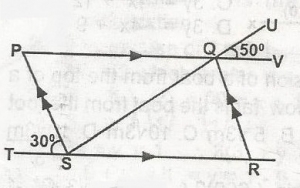
In the diagram, PQRS is a parallelogram. Find the value of < SQR
30o
50o
80o
100o
Correct answer is D
SQR + RQV + VQU = 18o angle on a straight line SP is parallel to QR and PV is parallel to TR
< STP = < RQV = 30o
But SQR + 30o + 50o = 180o
SQR = 180 - 80
= 100o
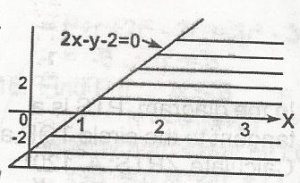
Find the inequality which represents the shaded portion in the diagram
2x - y - 2 \(\geq\) 0
2x - y - 2 \(\leq\) 0
2x - y - 2 < 0
2x - y - 2 > 0
Correct answer is A
2x - y - 2 \(\geq\) 0 = y \(\leq\) 2x - 2
when x = 0, y = -2, when y = 0, x = 1
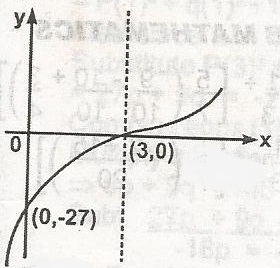
y = (x - 3)3
y = (x + 3)3
y = x3 - 27
y = -x3 + 27
Correct answer is C
y = x3 - 27, y = -27 \(\to\) (0, -27)
when y = 0, x = 3 (3, 0)
JAMB Subjects
Aptitude Tests