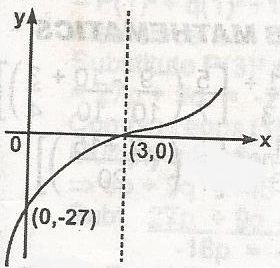
y = (x - 3)3
y = (x + 3)3
y = x3 - 27
y = -x3 + 27
Correct answer is C
y = x3 - 27, y = -27 \(\to\) (0, -27)
when y = 0, x = 3 (3, 0)
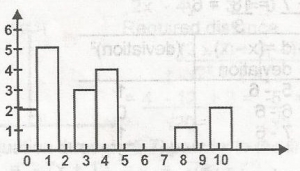
The bar chart shows the distribution of marks in a class test. How many students took the test?
15
20
25
30
Correct answer is B
Number f students that took the test = \(\sum f\). Where f is the frequencies
= 2 + 5 + 0 + 3 + 4 + 0 + 0 + 2 + 3 + 1 + 2 = 20
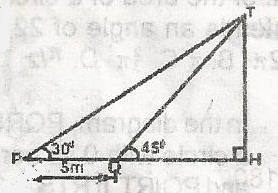
From the figure, calculate TH in centimeters
\(\frac{5}{\sqrt{3} + 1}\)
\(\frac{5}{\sqrt{3} - 1}\)
\(\frac{5}{\sqrt{3}}\)
\(\frac{\sqrt{3}}{5}\)
Correct answer is B
TH = tan 45o, TH = QH
\(\frac{TH}{5 + QH}\) = tan 30o
TH = (b + QH) tan 30o
QH = 56 (5 + QH) \(\frac{1}{\sqrt{3}}\)
QH(1 - \(\frac{1}{\sqrt{3}}\)) = \(\frac{5}{\sqrt{3}}\)
QH = \(\frac{5\sqrt{3}}{\sqrt{3}} - \frac{1}{\sqrt{3}}\)
= \(\frac{5}{\sqrt{3} - 1}\)
6cm
7cm
8cm
9cm
Correct answer is C
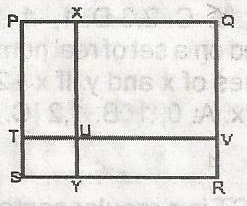
Since area of square PQRS = 100cm2
each lenght = 10cm
Also TUYS : XQVU = 1 : 16
lengths are in ratio 1 : 4, hence TU : UV = 1: 4
Let TU = x
UV = 1: 4
hence TV = x + 4x = 5x = 10cm
x = 2cm
TU = 2cm
UV = 8cm
But TU = SY and UV = YR
YR = 8cm
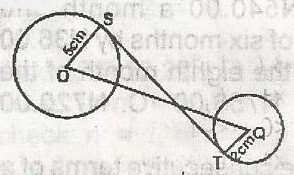
7 \(\sqrt{3}\)cm
12.9cm
\(\sqrt{87}\)cm
7cm
Correct answer is B
SQ2 + OS2 = OQ2 + 52 = 142
SQ2 = 142 - 52
196 - 25 = 171
ST2 + TQ2 = SQ2
ST2 + 22 = 171
ST2 = 171 - 4
= 167
ST = \(\sqrt{167}\)
= 12.92 = 12.9cm
JAMB Subjects
Aptitude Tests