20
21
15
18
Correct answer is A
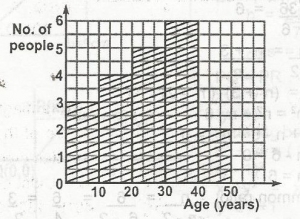
\(\begin{array}{c|c} \text{Age in years} & 10 & 20 & 30 & 40 & 50 \\\hline \text{frequency} & 3 & 4 & 5 & 6 & 2\end{array}\)
\(\sum f \) = number of people involved in the pollution
\(\sum f\) = 3 + 4 + 5 + 6 + 2 = 20
20o
40o
10o
30o
Correct answer is B
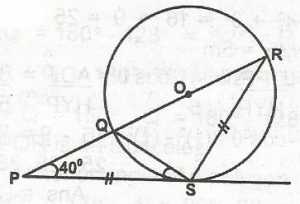
PS = SR
\(\bigtriangleup\)PSR is an isosceles
< P = < SPQ = 40°
< R = < SRQ
< PSQ = < SRQ (alternate segment)
< PSQ = 40°
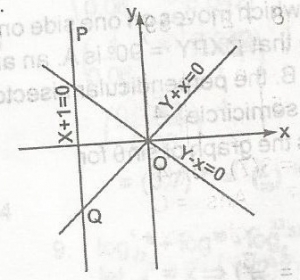
Triangle OPQ is the solution of the inequalities
x - 1 < 0, y + \(\geq\) 0, y - x \(\geq\) 0
x + 1 \(\leq\) 0, y + x \(\geq\) 0, y - x \(\leq\) 0
x - 1 \(\geq\) 0, y - x \(\geq\) 0, y + x \(\geq\) 0
y + x \(\geq\) 0, y - x \(\leq\) 0
Correct answer is B
No explanation has been provided for this answer.
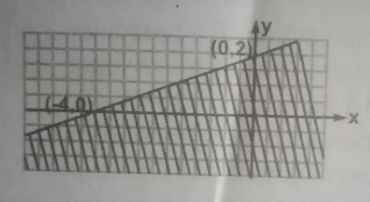
Use the graph find the values of p and q if px + qy \(\geq\) 4
p = 2, q = -1
p = -1, q = 2
p = 2, q = 2
p = 1, q = 2
Correct answer is B
m = \(\frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 0}{0 - (4)} = \frac{2}{4} = \frac{1}{2}\)
\(\frac{y_2 - y_1}{x_2 - x_1} \geq m\)
\(\frac{y - 0}{x + 4} \geq \frac{1}{2}\)
2y \(\geq\) x + 4, -x + 2y \(\geq\) 4 = px + qy \(\geq\) 4
p = -1, q = 2

17
16
15
14
Correct answer is A
\(\begin{array}{c|c} \text{no. of passengers} & \text{Number of taxis}\\ \hline 0.5 - 2.5 & 3\\ 2.5 - 4.5 & 4 \\ 4.5 - 6.5 & 7\\ 6.5 - 8.5 & 5\\ 8.5 - 10.5 & 4 \\ 10.5 - 12.5 & 1\\ \hline \text{Total} & 24 \end{array}\)
Thus, the taxi with more than 4 passengers
= 7 + 5 + 4 + 1 = 17
JAMB Subjects
Aptitude Tests