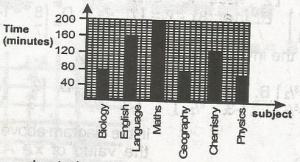
460mins
720mins
960mins
200mins
Correct answer is B
80 + 160 + 200 + 80 + 128 + 72 = 720minutes
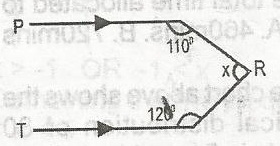
The value x in the figure given is
110o
100o
70o
130o
Correct answer is D
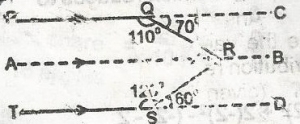
Sum of the angles in a triangle = 180°
180° - x + 60 + 70 = 180
130° - x = 180° - 180° = 0°
x = 130°
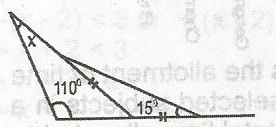
In the diagram given, find the value of x.
30o
40o
45o
15o
Correct answer is B
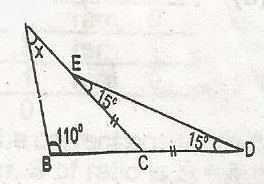
In the diagram above, < CDE = < CED = 15o
(base < s of isos. \(\bigtriangleup\))
< ECD = 180o - (15 + 15)o
= 180o - 30o = 150o
But x + 110o = 150o
(Sum of opp. interior < s of a\(\bigtriangleup\) = opp. exterior < )
x = 150o - 110o = 40o
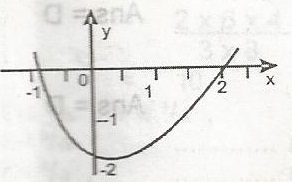
The graph above is correctly represented by
y = x2 - x - 2
y = x2 - 3x + 2
y = x2 - x - 1
y = x2 + x - 2
Correct answer is A
The graph crosses the x-axis at x = -1 and x = 2
Thus, x + 1 = 0 and x - 2 = 0
x\(^2\) - 2x + x - 2 = 0
x\(^2\) - x - 2 = 0
giving y = x\(^2\) - x - 2
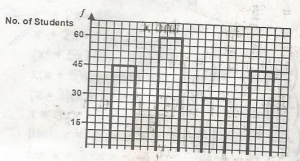
180
135
210
105
Correct answer is A
45 + 60 + 30 + 45 = 180 students.
JAMB Subjects
Aptitude Tests