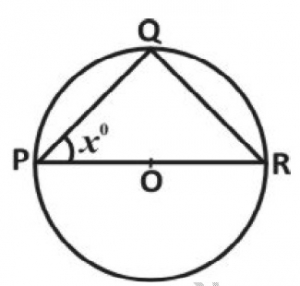
In the diagram above, PQR is a circle centre O. If < QPR is x°, find < QRP.
x°
(90 – x)°
(90 + x)°
(180 – x)°
Correct answer is B
< PQR = 90° (angle in a semi-circle) < QRP = (90 - x)°
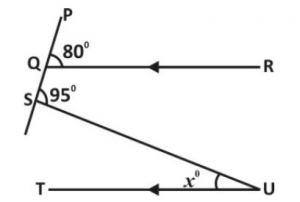
In diagram above, QR//TU, < PQR = 80° and < PSU = 95°. Calculate < SUT.
15o
25o
30o
80o
Correct answer is A
< PQR = < PTU = 80°
< TSU = 85°
x = 180° - (80° + 85°)
= 15°
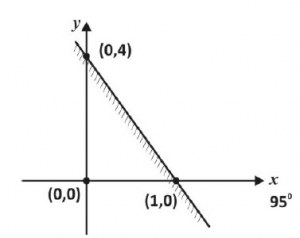
The shaded region above is represented by
the equation
y ≤ 4x + 2
y ≥ 4x + 2
y ≤ -4x + 4
y ≤ 4x + 4
Correct answer is C
Equation of the line
\(\frac{y - 4}{x - 0} = \frac{0 - 4}{1 - 0}\)
\(\frac{y - 4}{x} = \frac{-4}{1}\)
\(\therefore -4x = y - 4\)
\(y = -4x + 4\)
\(\therefore \text{The shaded portion = } y \leq -4x + 4\)
N42,000
N18,000
N16,000
N12,000
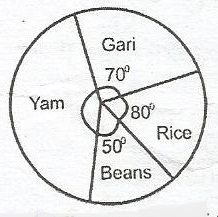
Correct answer is C
Angle of sector subtended by yam
= 360o - (70 + 80 + 50)o
= 360o - 200o
= 160o
But \(\frac{80^o}{360^o}\) x T = 8000
T = \(\frac{8000 \times 360^o}{80^o}\)
= N36,000
Hence the amount spent on yam = \(\frac{160^o}{260} \times N36,000\)
= N16,000
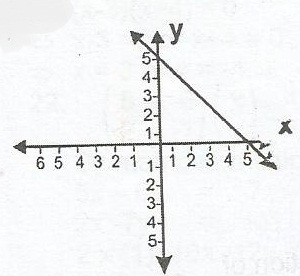
y = x + 5
y = -x + 5
y = x - 5
y = -x - 5
Correct answer is B
(x1, y1) = (0,5)
(x2, y2) = (5, 0)
Using \(\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}\)
\(\frac{y - 5}{0 - 5} = \frac{x - 0}{5 - 0}\)
\(\frac{y - 5}{-5} = \frac{x}{5}\)
5(y - 5) = -5x
y - 5 = -x
x + y = 5
y = -x + 5
JAMB Subjects
Aptitude Tests