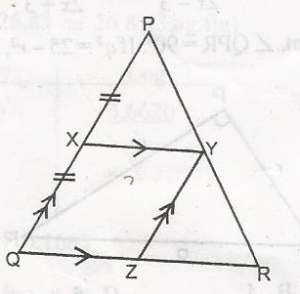
In the figure /PX/ = /XQ/, PQ//YZ and XV//QR. What is the ratio of the area of XYZQ to te area of △YZR?
1:2
2:1
1:2
3:1
Correct answer is B
From the diagram, XYZQ is a parallelogram. Thus, |YZ| = |XQ| = |PX|; △PXY, Let the area of XYZQ = A1, the area of △PXY
= Area of △YZR = A2
Area of △PQR = A = A1 + 2A2
But from similarity of triangles
Area of PQRArea of PXY=(PQPX)2=(QRXY)2
AA2=(21)2=21
A = 4A2 But, A = A1 + 2A
A1 = 4A2 - 2A2
A1 = 2A2
A1A2 = 2
A1:A2 = 2:1
Area of XYZQ:Area of △YZR = 2:1
Similar Questions
Find the value of x for which x−5x(x−1) is defined...
If P = {3, 5, 6} and Q = {4, 5, 6} then P∩Q equals ...
If A = (−3,5) and B = (4,−1) find the co-ordinate of the mid point ...
A binary operation ∗ is defined on a set of real numbers by x ∗ y = xy for all real va...
Given that p13 = 3√qr, make q the subject of the equation...
The angles marked in the figure are measured in degrees. Find x. ...