In the figure, PS = RS = QS and QRS = 50°. Find QPR
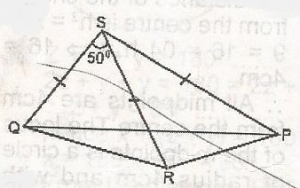
In the figure, PS = RS = QS and QRS = 50°. Find QPR
25O
40O
50O
65O
Correct answer is A
In the figure PS = RS = QS, they will have equal base QR = RP
In angle SQR, angle S = 50O
In angle QRP, 65 + 65 = 130O
Since RQP = angle RPQ = \(\frac{180 - 130}{2}\)
= \(\frac{50}{2} = 25^o\)
QPR = 25°
Similar Questions
Simplify: \((\frac{1}{4})^{-1\frac{1}{2}}\)...
Solve the equation 4/a + 1/5a = 3 ...
Find the value of (0.006)3 + (0.004)3 in standard form...
From the graph determine the roots of the equation y = 2x2 + x - 6 ...
In the diagram, GI is a tangent to the circle at H. If EF||GI, calculate the size of ∠EHF ...
What is the value of x when y = 5? y = \(\frac{1}{2}\) x + 1...
Find the product of 0.0409 and 0.0021 leaving your answer in the standard form ...