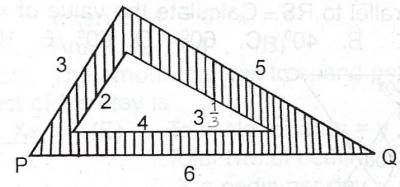
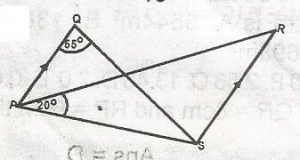
Area of shaded portion = Area of triangle PQR - Area of inner triangle
Area of triangle given 3 sides a, b, c = \(\sqrt{s(s - a)(s - b)(s - c)}\)
where \(s = \frac{a + b + c}{2} \)
Area of PQR :
\(s = \frac{3 + 5 + 6}{2} = \frac{14}{2} = 7\)
Area = \(\sqrt{7(7 - 3)(7 - 5)(7 - 6)}\)
= \(\sqrt{7(4)(2)(1)} = \sqrt{56}\)
\(\implies K^{2} = \sqrt{56}\)
Area of inner triangle :
\(s = \frac{2 + 4 + \frac{10}{3}}{2} = \frac{14}{3}\)
Area = \(\sqrt{\frac{14}{3} (\frac{14}{3} - 2)(\frac{14}{3} - 4)(\frac{14}{3} - \frac{10}{3})}\)
= \(\sqrt{\frac{14}{3} (\frac{8}{3})(\frac{2}{3})(\frac{4}{3})}\)
= \(\sqrt{\frac{896}{81}}\)
= \(\sqrt{\frac{16}{81}} \times \sqrt{56}\)
= \(\frac{4}{9} K^{2}\)
\(\therefore \text{The area of the shaded portion} = K^{2} - \frac{4}{9}K^{2} = \frac{5}{9}K^{2}\)