Processing math: 100%

WAEC Mathematics Past Questions & Answers - Page 94

466.

Simplify: $\sqrt{12} ( \sqrt{48} - \sqrt{3}$ )

Correct answer is A

$\sqrt{12} ( \sqrt{48} - \sqrt{3}$ )

$\sqrt{4 \times 3} (6 \times 3 - \sqrt{3}) = 2 \sqrt{3}(4 \sqrt{3} - \sqrt{3})$

= 2 $\sqrt{3} \times \sqrt{3} (4 - 1) 2\sqrt{9}(3) = 2 \times 3 \times 3 = 18$

467.

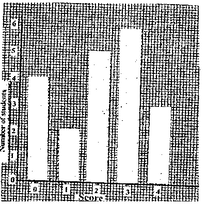
The bar chart above shows the scores of some students in a test. Use it to answer this

If one student is selected at random, find the probability that he/she scored at most 2 marks

$\frac{11}{18}$

$\frac{11}{20}$

$\frac{7}{22}$

$\frac{5}{19}$

View answer & explanation

Correct answer is B

at most 2 marks = 5 + 2 + 4 students = 11 students

probability(at most 2 marks) = $\frac{11}{20}$

468.

The volume of a cube is 512cm³. Find the length of its side

6cm

7cm

8cm

9cm

View answer & explanation

Correct answer is C

volume of cube = L x L x L

512cm³ = L³

L³ = 512cm³

L = 3 $\sqrt{512}$

L (512)^{$\frac{1}{3}$}

= (2⁹)^{$\frac{1}{3}$}

2³ = 8cm

469.

If 23_x = 32₅, find the value of x

View answer & explanation

Correct answer is A

23_x = 32₅

2 $\times x^1 + 3 \times x^0 = 3 \times 5^1 + 2 \times 5^0$

= 2x + 3 = 15 + 2

2x + 3 = 17

2x = 17 - 3

2x = 14

x = $\frac{14}{2}$

x = 7

470.

Simplify 10 $\frac{2}{5} - 6 \frac{2}{3} + 3$

6 $\frac{4}{15}$

6 $\frac{11}{15}$

7 $\frac{4}{15}$

7 $\frac{11}{15}$

View answer & explanation

Correct answer is B

10 $\frac{2}{5} - 6 \frac{2}{3} + 3$

$\frac{52}{5} - \frac{20}{3} + \frac{3}{1}$

= $\frac{156 - 100 + 45}{15}$

$\frac{156 + 45 - 100}{15}$

= $\frac{201 - 100}{15}$

= $\frac{101}{15}$

= 6 $\frac{11}{15}$